WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Geluidsgolven(Cosinus functie)

Ik ben op het moment bezig met mijn praktische opdracht wiskunde waarbij ik voor een elementaire trilling de volgende functie krijg:
A cos (wt+F)
Hierbij is A de amplitude(het volume)
w is de frequentie · 2p
en F is de fasehoek in radialen.
Nu kan ik uit de A en de w wel komen maar ik heb geen flauw idee wat een fasehoek precies is.
Zou iemand mij kunnen uitleggen wat een fasehoek is?
alvast bedankt!

Pieter

Pieter
Leerling bovenbouw havo-vwo - donderdag 5 april 2007

Antwoord

Een cosinusfunctie, bijvoorbeeld f(x)=cos(x) of g(t)=cos(wt) begint op x=0 danwel wt=0 altijd op 'startwaarde' 1. Immers: cos(0)=1
dat is hieronder de zwarte lijn:

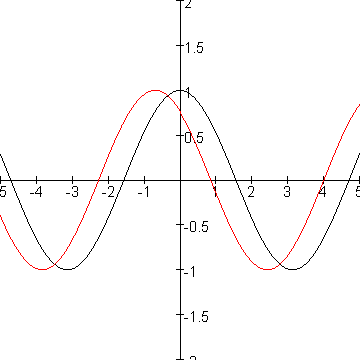
Echter, een willekeurige harmonische golffunctie, in de vorm van een cosinus hoeft op t=0 niet per-sé op 1 te beginnen. Dat is het geval als de cosinusfunctie verschoven is. Zie de rode lijn.
Nu is de waarde van f het bedrag dat we bij de wt moeten optellen om de cosinusgrafiek in de x-richting te verschuiven.
Let op: wanneer we een positief bedrag bij wt optellen, dan verschuift de grafiek daardoor naar links. En wanneer f negatief is, verschuift de grafiek naar rechts. Kun je zien waarom dat is?

We kunnen het ook op een andere manier begrijpen, namelijk met behulp van de eenheidscirkel:

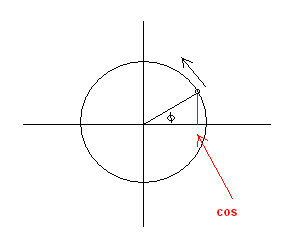
Bij een bepaalde hoek (hier f) hoort een punt op de eenheidscirkel. Nu is de projectie op de x-as de cosinuswaarde. (en de projectie op de y-as van het punt is de sinuswaarde van de hoek)
Als we kijken naar cos(wt), is wt de hoek. Die begint op t=0 met waarde 0. (projectie op de x-as is dan 1, en dus is de cosinus ook 1) En daarna wordt wt alsmaar groter. (de hoek gaat dus op de eenheidscirkel rondjes draaien, tegen de wijzers van de klok in.)
En het eerste wat gebeurt vanaf t=0 is dat de cos-waarde kleiner wordt.
Nu: doordat we uitgaan van cos(wt+f) is op t=0 de startwaarde van het argument van de cosinus gelijk aan f. Hierdoor heeft op t=0 de cosinus al een andere waarde dan de standaardwaarde 1. Vrij vertaald: hij is al een eindje op dreef met kleiner te worden. Precies zoals je ook in de grafiek kon zien.

groeten,
martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 5 april 2007