WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Hoek en afstand van vlak en lijn

Dit is een reactie op vraag 49873

Bedankt, nu begrijp ik 27c en e, maar ik snap 12 nog niet.
Ten eerste, is de methode die ik gebruik voor de berekening van afstand punt tot lijn goed? = '1.Hulpvlak vinden waarin punt B(gegeven), punt B'het dichtstbij kan projecteren. In dit vlak moet een lijn zijn van de gegeven vlak. 2.Teken deze hulpvlak, teken de loodrechte lijn van punt tot lijn(van vlak). 3.Bereken m.b.v. zijde*hoogte methode BB'.

Wat bedoelt u met 'ABFE staat niet loodrecht op ADE', is mijn methode niet genoeg? En ik snap niet hoe vlak EFF'E' loodrecht staat op AED?
Kucuko
Leerling bovenbouw havo-vwo - vrijdag 23 maart 2007

Antwoord

Nou, daar ben ik weer.

Makkelijk vind ik die opgave ook niet.
Maar, met je methode is echt iets aan de hand. In mijn opzet is de eerste stap: 1.Hulpvlak vinden waarin punt B(gegeven) ligt en die loodrecht op het gegeven vlak staat. In dit hulpvlak ligt automatisch een lijn van de gegeven vlak.

Het is echt belangrijk dat het hulpvlak loodrecht op het gegeven vlak staat. Kijk maar eens wat er gebeurt als je de afstand van E tot het vlak ABCD wilt berekenen. Dat is natuurlijk gewoon de afstand van E tot E'. Maar het vlak ADE, CDE of ABE zul je dat punt (en dus ook de kortste afstand niet vinden). Dat lukt alleen met het vlak EFF'

Aangezien het m.i. een beetje moeilijk is heb ik de opgaven maar een stuk uitgewerkt.

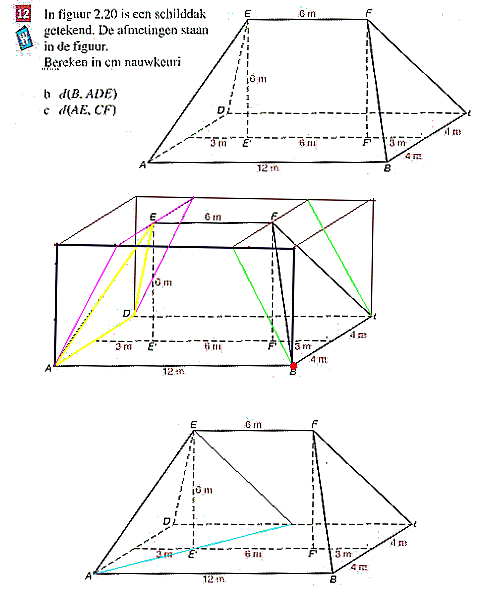
Bij de 12 heb ik het hele blok om het dak geteken. Dat doe je b.v. door EE' te verschuiven tot dat het in A begint. En in B, C en D. Daarna het vlak ABCD verschuiven tot het bovenaan die lijnen zit. Het vlak ADE wordt dan wat duidelijker door AD te verchuiven tot het E snijdt. Je krijgt dan het paarse vlak.
Maar het gaat om het donkrblauwe vlak. EFF'E' staat loodrecht op AD. AD ligt in ADE. Dus EFF'E' staat loodrecht op ADE. Als je dit evenwijdig verschuift tot het B snijdt krijg je het donkerblauwe hulpvlak. De snijlijn van ADE met dit hulpvlak is paars. In dat hulpvlak kun je het vervolgens prima oplossen. Eigenlijk kijk je dan gewoon naar het zijaanzicht.

Opgave c gaat over de afstand tussen twee kruisende lijnen. De aanpak hiervan (dat staat vast ergens in je hoofdstuk) is: 1) Een vlak tekenen door de ene lijn, evenwijdig aan de andere. 2) Nu neem je een willekeurig punt van de andere lijn en berekent de afstand tot het bepaalde vlak. Daarvoor maak je weer een hulpvlak zoals hierboven.
1) doe ik hier door de lijn CF evenwijdig te verschuiven tot hij door E gaat (paarse lijn). Teken de blauwe lijn erbij en je ziet dat dit vlak loodrecht op het vlak ABCD staat. Dus bij 2) neem je als hulpvlak ABCD en berekent daarin de afstand tot de blauwe lijn.

Nou, ik heb een beetje te veel verklapt. Maar, ik hoop dat je het zo ziet en dat je in je hoofdstuk nog andere opgaven hebt om te zien hoe je deze afstanden moet berekenen.

Groet. Oscar

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 24 maart 2007