|
|
|
\require{AMSmath}
Vereenvoudigen mbv iteratie
Gegeven:
f(x)=1+(1/√(1+x2))·e^(-x($\pi$/2+arctan(1/x)))
Deze vergelijking kan mbv iteratie vereenvoudigt worden tot:
f(x)$\approx$1,0202+0,9798·e^(-3,0182·x)
Ik heb geen ervaring met itereren en vraag mij af hoe deze vereenvoudiging tot stand is gekomen. Heeft u misschien een tip?
gerwin
Student hbo - woensdag 21 maart 2007
Antwoord
Beste Gerwin,
Het heeft even geduurd. Je vraag is intrigerend. Maar, we komen er nog niet achter wat je voor iteratie bedoelt. Er zijn veel vormen van iteratie en reeksontwikkeling. Kun je iets meer over de achtergrond vertellen.
Wel al vast een paar dingen: arctan(1/x) = p/2-arctan(x). Dat maakt de formule alvast wat eenvoudiger.
Verder 1,0202  1+2/99 en 0,8789 1-2/99. Maar de herkomst van de 3,0182 is niet duidelijk, behalve dat het in de buurt van p zit.
Ten slotte is het wel een behoorlijke benadering maar niet zo goed als het aantal decimalen suggereert. Zie het onderstaande plaatje. Op het onderste plot staat het verschil tussen de formule en de benadering.
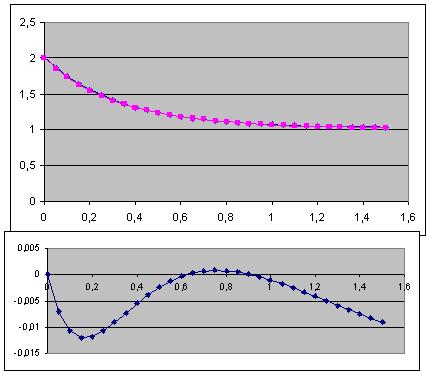
Ik hoop meer van je te horen. Groet. Oscar
os
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 25 maart 2007
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
