WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Minimale oppervlakte van een bloempot

Ik wil de minimale oppervlakte van bloempotten berekenen. De inhoud moet steeds 1 dm³ zijn.

1e vraag:
regelmatige 3-hoek met verticale wanden

2e vraag:
afgeknotte piramide (op zijn kop) met de hoek tussen de wanden en de grond 75 graden

3e vraag:
zelfde als vraag 2 met hoek = 60 graden
thomas
Leerling bovenbouw havo-vwo - maandag 19 maart 2007

Antwoord

1.
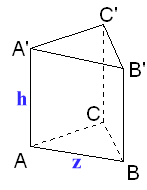Kies voor de lengte van een zijde van het grondvlak van je prisma z. De inhoud van een recht prisma is gelijk aan G·h waarbij G de oppervlakte is van het grondvlak en h de hoogte. Omdat je al weet dat de inhoud 1 dm³ is kan je h uitdrukken in z. Je kunt dan een formule maken voor de oppervlakte van de bloempot (grondvlak plus drie maal een zijkant) uitgedrukt in z. De oppervlakte moet minimaal worden, dus differentiëren, nul stellen, tekenverloop maken en hopen dat je een minimale waarde vindt voor z.

2.
Deze vraag is iets lastiger, maar doe eerst dan de 1e vraag maar en dan reageer je maar op deze vraag dan geef ik je nog wat hints voor de afgeknotte piramide.

3.
Zie vraag 2.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 21 maart 2007