|
|
|
\require{AMSmath}



Driehoeken oplossen
Hallo ik heb een vraagje.
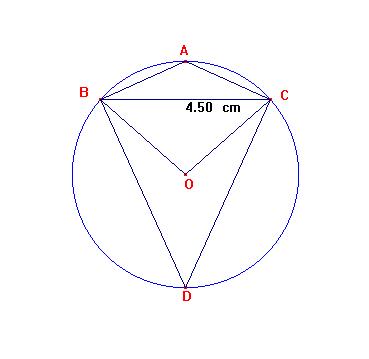
1. Teken in een cirkel met straal 3 cm de koorde [BC] zodat |BC|=4.5 cm
2. Teken met [BC] als basis de gelijkbenige driehoeken zodat c(O,3) de omgeschreven cirkel is van de driehoeken.
3. Los de driehoeken op.
De eerste en tweede vraag lukken wel maar bij de derde weet je alleen dat de basis 4.5 cm is maar verder heb je geen gegevens.
Hoe moet ik verder?
Alvast bedankt
Kevin
2de graad ASO - maandag 5 maart 2007
Antwoord
Dag Keven
Noem D de tophoek van de gelijkbenige driehoek met de grootste hoogte, en A de tophoek van de gelijkbenige driehoek met de kleinste hoogte.
Van de driehoek OBC ken je de drie zijden.
Met behulp van de cosinusregel kun je dus de hoek BOC berekenen.
Dit is de middelpuntshoek op de koorde BC.
De hoek BDC is dan de omtrekshoek op dezelfde koorde. Dus deze hoek kun je ook berekenen.
De hoeken DBA en DCA zijn recht (waarom?)
Dus ken je ook de hoek BAC.
Als je de tophoeken van een gelijkbenige driehoek kent, ken je ook de basishoeken.
Met de sinusregel kun je in beide driehoeken de opstaande zijden berekenen.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 5 maart 2007
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|










