|
|
|
\require{AMSmath}



Taxistandplaats
De gehele vraag luidt: Een taxistandplaats wordt gemiddeld door 3 taxi's in een uur aangedaan. De tussentijden van het binnenkomen van de taxi's hebben een negatief exponentiele verdeling. - Bepaal de tijd dat je gemiddeld op een taxi moet wachten.
- Bepaal vervolgens de kans dat je langer dan een half uur op een taxi moet wachten.
Uit de eerste vraag kan ik als antwoord: 1/3 halen en dat is volgens mij ook wel goed.
v. laa
Ouder - donderdag 24 oktober 2002
Antwoord
Laten we eens wat dingen op een rijtje zetten, anders blijft die taxi ons maar achtervolgen. De negatief exponentiŽle verdeling kan je opvatten als: hoe lang duurt het totdat een 'succes' optreedt. Een typisch voorbeeld is de tijd die zal verstrijken tot de eerstvolgende telefoonoproep wanneer er gemiddeld l oproepen per tijdseenheid zijn.
Theorie
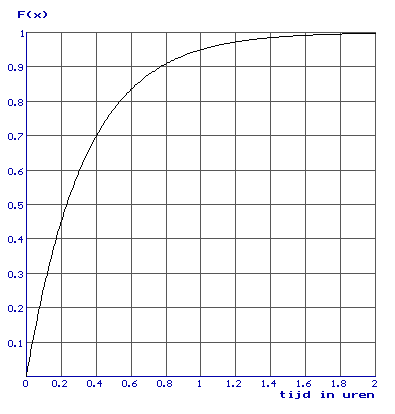
Als T een continue stochastische variabele is dan heeft T de volgende kansdichtheid:
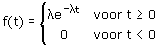
..dan is T negatief exponentiŽel verdeeld met gemiddelde en variantie:
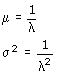
Voorbeeld
Laten we voor l=3 de grafiek maar eens tekenen:
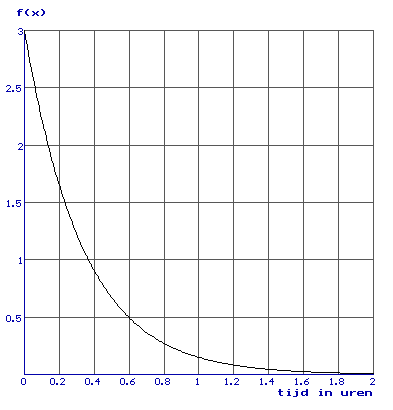
Hierboven is net als bij de 'normaal verdeling' de oppervlakte onder de grafiek precies 1. Als je de kans wilt weten dat je op z'n hoogst 0,4 uur moet wachten dan zou je de oppervlakte onder de grafiek moeten bepalen van 0 tot 0,4:
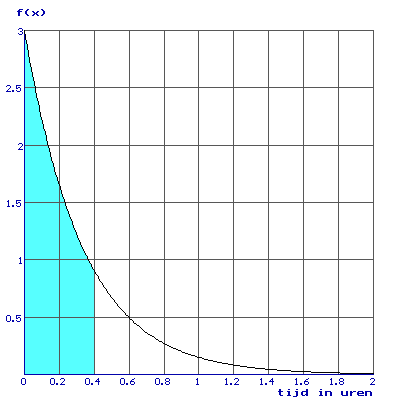
Dat is natuurlijk niet handig, zodat men voor de oppervlakte onder grafiek (links!) een formule heeft bedacht (dit is de integraal uit de vorige antwoorden!):
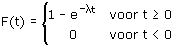
Laten we daar nu ook de grafiek voor l=3 eens tekenen:
Hierin kan je bijvoorbeeld aflezen dat de kans dat je hoogstens 0,4 uur moet wachten gelijk is aan 0,7.
Wat is nu de kans dat je langer moet wachten dan 0,4 uur?
Antwoord: P(T>0,4)=1-P(T 0,4)=1-0,7=0,3 0,4)=1-0,7=0,3
Deze kans kan je natuurlijk ook uitrekenen! Wat is nu de kans dat je langer moet wachten dan 0,4 uur?
Antwoord: P(T>0,4)=1-P(T 0,4)=1-(1-e-3∑0,4)=0,301 0,4)=1-(1-e-3∑0,4)=0,301
..en dan kan je het volgens mij nu zelf. Daar heb ik geen Excelblad voor nodig..., maar misschien kan je dat nu zelf ook wel bedenken.
Zie Negatief exponentiŽle verdeling

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 26 oktober 2002
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








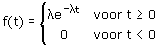
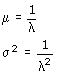


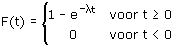

 0,4)=1-0,7=0,3
0,4)=1-0,7=0,3 
