WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Poissonformule

Ik ben bezig met een praktische opdracht over de Poissonverdeling en ik loop al vast bij punt 2, die luidt 'wat is de poissonformule met betrekking tot de poissonverdeling? geef uitleg over de formule.' nu snap ik niet wat het verschil is tussen de formule en de verdeling.
En als iemand mij dan ook zou willen helpen met punt 3, die luidt 'Onderzoek onder welke voorwaarden een binominaal verdeelde toevalsvariabele benaderd mag worden door een poissonverdeelde toevalsvariabele.', zou ik érg dankbaar zijn! Ik zou bij dat laatste willen weten hoe ik het moet onderzoeken. Alvast bedankt voor de moeite!
mara
Leerling bovenbouw havo-vwo - donderdag 22 februari 2007

Antwoord

De eerste vraag is ook redelijk onduidelijk gesteld.
In ieder geval kan ik met de Poissonformule losse kansen berekenen. Wanneer ik al die losse kansen in een grafiek zet krijg ik de grafiek van een Poissonverdeling. Nou ja..... of het dat moet zijn weet ik niet.

Nu kan je de Poissonverdeling als uitgangsverdeling gebruiken. Wanneer je bijvoorbeeld kijkt naar het aantal klanten dat in een uur bij het postkantoor binnenkomt. Hieruit kan je nog het een en ander meer afleiden (wachtrijen en zo). Dus het eerste bestaansrecht van een Poissonverdeling is als afzonderlijke kansverdeling.

Daarnaast kan de Poissonverdeling (onder bepaalde voorwaarden) gebruikt worden om een binomiale verdeling mee te benaderen. Hier vraag je naar. Zo'n benadering werkt wanneer beide verdelingen nagenoeg dezelfde vorm hebben. Dan geven ze namelijk ook dezelfde kansen als uitkomsten.
Zelf hanteer ik voor het benaderen van een binomiaal verdeling met een poisson het criterium n·p 5.
Dan verder ook (na enige aanpassing) n·q 5 (zelf uitzoeken hoe dat zit) ....... dus een van deze twee.
Veel leuker is het om zelf eens te onderzoeken waarom de benadering goed is.
Ik neem maar eens Binomiaal met n=50 en p=0,03 en bijbehorend Poisson met m=n·p = 1,5.

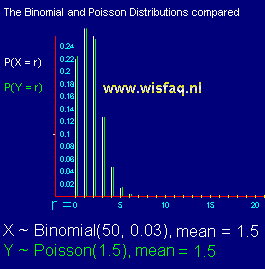
Je ziet hoe sterk de verdelingen nu overeenkomen. Probeer hetzelfde eens met p=0,30......
Het appletje bij de onderstaande link maakt het mogelijk om zelf eens wat te proberen.

Met vriendelijke groet
JaDeX
Zie Binomiale verdelingen benaderen

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 24 februari 2007