WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Cirkelprobleem

Laat ABC een driehoek in een cirkel, met de punten ABC op de cirkel.

Laat p en q de stralen van twee cirkels door A, rakend aan BC in respectievelijk B en C. Toon aan dat geldt: pq = R²

Hoe kan ik dit aantonen? Ik heb al heel wat gepuzzeld maar kom er niet uit.
martij
Student hbo - dinsdag 6 februari 2007

Antwoord

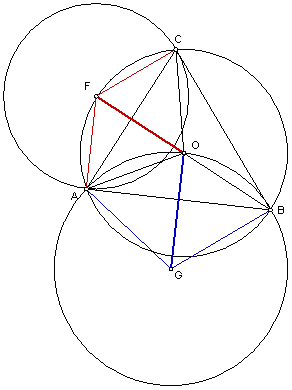
Merk op dat hoeken GBO en FCO gelijk zijn omdat GB en FC loodrecht op BC staan. Bovendien zijn hoeken GBO, FCO, BCO en CBO duidelijk samen 180° net als hoeken BCO, CBO en COB. Maar dat betekent dat GBO en FCO elk de helft zijn van COB, en dus gelijk aan hoek A.

Ook zien we dat hoek FOA = 1/2 hoek COA = hoek CBA. Dus zijn driehoeken FOA en FOC gelijkvormig aan ABC. Op soortgelijke manier is ook driehoek OGA gelijkvormig aan ABC.

De gelijkvormigheid van FOA en OGA levert de gevraagde vergelijking.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 6 februari 2007