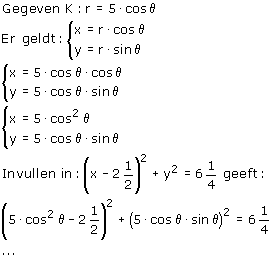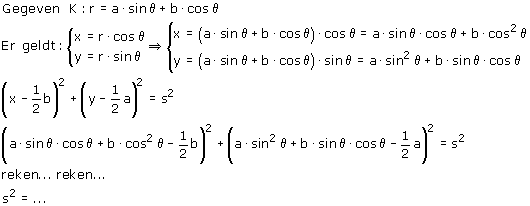WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Zijn de grafieken van deze poolvergelijkingen cirkels?

Dit is een reactie op vraag 48834

De precieze opdracht luidt:

De grafieken van de poolvergelijkingen
r=5sin(θ) met 0≤θ≤π
r=4cos(θ) met 0≤θ≤π
zijn cirkels. Bewijs dit.

daarbij hoort ook:

Geef een poolvergelijking van de cirkel met middelpunt (a ; b) en straal s en bewijs dat deze poolvergelijking inderdaad een cirkel oplevert.

Geef een poolvergelijking van de lijn y=ax+b en van de lijn x=c en gebruik deze vergelijkingen om snijpunten van grafieken van poolvergelijkingen met rechte lijnen te berekenen met de GR.

De enige basiskennis die we wel hebben gehad in ons boek is hoe je van normale coördinaten (x,y) naar poolcoördinaten (q,r) gaat.
Van die vermenigvuldigingsformule had ik inderdaad nog nooit gehoord.
Wel had ik als tip van mijn leraar gehad dat ik iets met
r²=x²+y² moest doen.
Verder moeten we alles zelf maar uitzoeken geloof ik, want het is een PO...

In iedergeval al hartstikke bedankt met die vermenigvuldigingsformules!!
Kunnen jullie me nog iets verder helpen?
Anna
Leerling bovenbouw havo-vwo - donderdag 25 januari 2007

Antwoord

Als je r=5·cosq plot op je GR zou je het vermoeden kunnen krijgen dat dit een cirkel is met middelpunt M(2¹/₂,0) en een straal r=2¹/₂. Dat vermoeden kan je zo controleren:

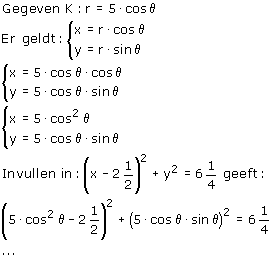
En dan nog even laten zien dat het klopt...

Hetzelfde kan je doen voor bijvoorbeeld r=4·sinq. Het gaat dan om een cirkel met M(0,2) en r=2. Zie je al hoe dat werkt? Je kunt het ook doen voor het algemene geval:

r=a·sinq+b·cosq

Je krijgt dan zoiets als:

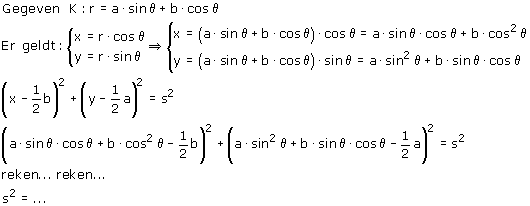
Werk dat maar 's uit! Je zult verrast zijn!

...en dan kan je wel weer verder denk ik...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 25 januari 2007