WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Poolvergelijkingen

Dit is een reactie op vraag 48752

Deze vraag boeit mij zeer. Graag wil ik aan u voorleggen of mijn uitwerking juist is.

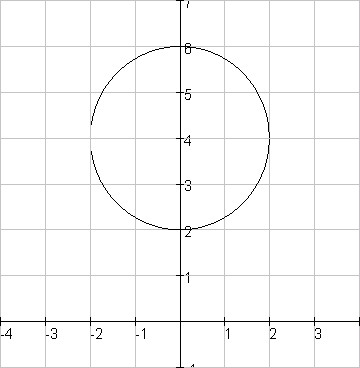
De poolvergelijking uitdrukken in een carthesische vorm geeft: r²-8y+12=0. De algemene vergelijking van een cirkel is r²=x²+y². Beide vergelijkingen verwerken in een stelsel geeft: r²=8y-12 Ù 8y-12=x²+y² Û -y²+8y-12=x². Stel nu x = 0 Û y²-8y+12=0 Û (y-2)(y-6)=0 Û y=2 Ú y=6. Dus op de cirkel liggen de punten (0,2) en (0,6). Het middelpunt is dus (0,4) en de straal is dus 2.
Tom
Leerling bovenbouw havo-vwo - dinsdag 23 januari 2007

Antwoord

Hallo Tom

Bij de omzetting naar de cartesische vergelijking stel je tegelijkertijd
r.sin(q)=y, (eventueel r.cos(q=x) en r² = x²+y²
Dus is de cartesische vergelijking : x² + y² - 8y + 12 = 0

Door x=0 te stellen zoek je de snijpunten met de y-as, deze zijn inderdaad (0,2) en (0,6)
De grafiek is :

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 24 januari 2007