WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Oplossen van een ongelijkheid

Dit is een reactie op vraag 48742

Ik ben er zelf ook niet onder de indruk van haha maar ik volg precies dat gene op wat er in het boek staat uitgelegd. Er staat namelijk dit:

'Het oplossen van gebroken ongelijkheden kan grafisch of algebraisch verlopen. (aangezien het gebruik van de GR bij ons verboden is moeten wij alles algebraisch doen). Er staat het volgende:

Algebraisch
LET OP: Bij ongelijkheden NOOIT kruislings vermenigvuldigen; de kans op fouten is 100%!
1. Herleid de ongelijkheid op 0
2. Bepaal de nulpunten van de teller en de noemer
3. Bepaal het tekenschema van de teller, de noemer, en van de hele breuk
4. Leid de oplossing af uit het tekenschema van de hele breuk.'

Om u duidelijk te maken hoe wij te werk moeten gaan kan ik wel even een voorbeeld overnemen uit het boek:

2x+7/x-1 ≥x+1 (x≠1)
2x+7/x-1 - (x+1)≥0 (x≠1)
2x+7/x-1 - ((x+1)(x-1))/x-1≥0
2x+7-(x²-1)/x-1≥0
-x²+2x+8/x-1≥0 (x≠1)

Nu bepaal je de nulpunten van de teller en de noemer:
-(x-4)(x+2)/x-1 Nulpunt teller: x=4 en x=-2
Nulpunt noemer: x=1

Nu bepaal je de tekenschema van de teller, de noemer en de hele breuk. Het antwoord is:
'Uit het tekenschema kun je afleiden dat de oplossing is: x in $<$1,4] dan wel x in $<$¬,-2].'

Als u snapt wat er staat, want ik niet helemaal, of een makkelijkere manier weet om dit op te lossen kunt u dat dan graag uitlegge?

Groetjes,
Serhan
Student hbo - zondag 21 januari 2007

Antwoord

Dat lijkt me een prima methode! Beter dan mijn methode! In je vorige vraag suggereerde je dat je moeite had met het laatste stapje... maar als ik dat zo zie zat je al een beetje vast in stap 1, maar dat is niet erg... Ik zal je eerste voorbeeld doen! OK?

$
\eqalign{
&Stap\,\,1.\cr
&\frac{{-10x+3}}
{{2x+1}}\leq2x+3\cr
&\frac{{-10x+3}}
{{2x+1}}-\left({2x+3}\right)\leq0\cr
&\frac{{-10x+3}}
{{2x+1}}-\frac{{\left({2x+3}\right)\left({2x+1}\right)}}
{{2x+1}}\leq0\cr
&\frac{{-10x+3}}
{{2x+1}}-\frac{{4x^2+8x+3}}
{{2x+1}}\leq0\cr
&\frac{{-10x+3-4x^2-8x-3}}
{{2x+1}}\leq0\cr
&\frac{{-4x^2-18x}}
{{2x+1}}\leq0\cr
&\frac{{4x^2+18x}}
{{2x+1}}\geq0\cr
&Stap\,\,2.\cr
&4x^2+18x=0\Rightarrow2x\left({2x+9}\right)=0\Rightarrow x=0\vee x=-\frac{9}
{2}\cr
&2x+1=0\Rightarrow x=-\frac{1}
{2}\cr}
$

Stap 3.

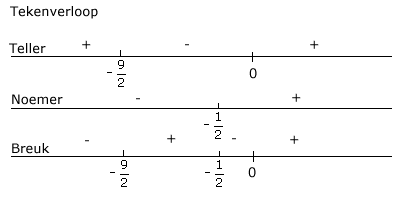
Stap 4.

$
\eqalign{
&We\,\,keken\,\,naar\,\,\frac{{4x^2+18x}}
{{2x+1}}\geq0\cr
&{Oplossing}:-\frac{9}
{2}\leq x<-\frac{1}
{2}\vee x\geq0\,\,\,dan\,\,wel:[-\frac{9}
{2},-\frac{1}
{2}>\cup[0,\to>\cr}
$

Nu heb ik wel een paar stappen gedaan zonder al te veel uitleg, probeer ze allemaal te volgen! Misschien is nu alles nog niet meteen duidelijk, maar kom je er zelf niet uit, dan horen we 't wel weer...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 21 januari 2007

Re: Re: Oplossen van een ongelijkheid