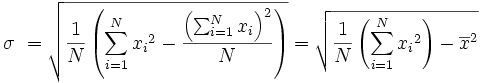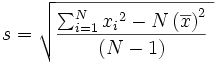WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Standaardafwijking en variantie

Dit is een reactie op vraag 48329

Het gemiddelde van beide reeksen is ook bekend. Ik heb de opdracht om Shewartkaarten (1e lijnscontrole) te automatiseren. Deze kaarten worden momenteel handmatig verwerkt, daarbij wordt een spreadsheet gebruikt voor de berekening van gem, stdev. Hierbij worden helaas veel fouten gemaakt. Dus vandaar automatiseren.

Ik heb dus kaart 1 gemiddelde=51,8, s1=8,1 en aantal(n)=30
vervolgens kaart 2 gemiddelde=49,9, s2=6,7 en aantal(n)=30

Vervolgens dienen de gegevens voor kaart 3 automatisch berekent te worden met de gegevens van kaart 1 en 2(samenvoegen dus),gem. = g1+g2/2, n wordt 60, maar voor de stdev gaat optellen en delen door 2 niet op, is het mogelijk om de nieuwe stdev voor kaart 3 te laten berekenen. Ik heb een viertal boeken statistiek erop nageslagen en internet geraadpleegd en kan niets vinden.

Alvast bedankt

Brigitte
Brigit
Student hbo - zaterdag 6 januari 2007

Antwoord

Op de Engelse Wikipedia: Standarddeviation staan bij Rapid Calculation methods deze formules:
Voor de populatie:

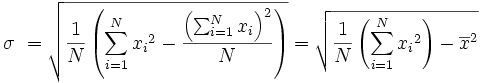
Voor de steekproef:

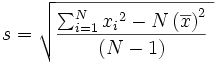
Deze formules geven aan hoe je de standaarddeviatie kunt berekenen als je de som van de kwadraten van de waarnemingen, het gemiddelde en N kent.
Omgekeerd kun je deze formules ook gebruiken om, gegeven de standaarddeviatie, het gemiddelde en N, de som van de kwadraten van de waarnemingen terug te vinden.
Voor de samengevoegde reeksen kun je dan de twee sommen van de kwadraten optellen en dan de formule weer gebruiken om de nieuwe standaarddeviatie te bepalen.
Ik heb mijn twijfels over de nauwkeurigheid als de standaarddeviaties sterk afgerond zijn weergegeven.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 6 januari 2007

Re: Re: Standaardafwijking en variantie