WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Lineaire differentiaalvergelijking eerste orde oplossen

Ik ben bezig met fysica (opladen van een condensator) maar het is het wiskunde deel waar ik nu op vastloop, ik begrijp niet helemaal wat er gebeurt.
Ik start van:
U - iR - q/C = 0
ik weet dat i = dq/dt dus:
U - R dq/dt - q/C = 0
en dan als oplossing:
q = UC (1-e^-t/RC)
wat zijn de tussenstappen? (die worden overgeslagen, maar.. ik geraak daar zelf echt niet uit)
Dan:
u(t) = U (1-e^-t/RC)
dit snap ik want je weet q/c =u
en uiteindelijk:
i(t) = U/R e^ t/RC
U/R = i, maar.. hoe het verder gaat..?^teller/_noemer^teller/_noemer
Suzann
Student universiteit - zondag 17 december 2006

Antwoord

Bij ieder circuit geldt op ieder moment dat als je een rondje maakt en uitkomt op hetzelfde punt (bijv. punt A) dat de som van de potentiaalverschillen NUL is.

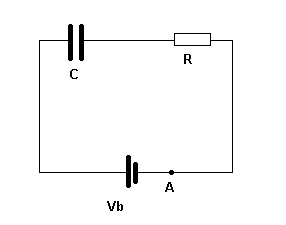
Dus vanuit A gaan we naar links en komen we langs de bron (Vb omhoog), dan langs de condensator (V=)Q/C omlaag, en tot slot langs de weerstand (V=)IR omlaag.
åV=0 Û +Vb -Q/C -IR = 0
dat is de achtergrond.

ofwel in jouw symbolen: U-iR-q/C=0
met q=q(t) de lading op de condensator.
Rdq/dt+q/C=U Û
dq/dt +q/RC = U/R

de oplossing van deze dv is de som van de homogene vergelijking
(dq/dt +q/RC = 0) en een particuliere oplossing van dq/dt +q/RC = U/R
eerst de homogene vergelijking:
q(t)=A.exp(-t/RC)
en een particuliere oplossing is q(t)=UC

hieruit volgt: q(t)=A.exp(-t/RC)+UC
nu moeten we nog A bepalen. die volgt uit de beginvoorwaarde. Deze heb je niet genoemd, maar die zal zijn dat op t=0 de condensator een lading nul heeft: q(0)=0. hieruit volgt dat A=-UC
En dus: q(t) = UC.(1-exp(-t/RC))

dan het potentiaalverschil over de condensator: V=q/C
ofwel U(t)=U.(1-exp(-t/RC))

Je mag dus niet zeggen i=U/R want dan heb je het potentiaalverschil over de condensator, en die zet je over de weerstand.
Nee, om i te berekenen moet je gebruik maken van
i=dq/dt
want de verandering van lading op de condensator is namelijk ook de lading die op dat moment door het gehele circuit aan het stromen is.
i(t)=dq/dt = (U/R).exp(-t/RC)

groeten,
martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 18 december 2006