WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Soort punt, discontiuiteit

gegroet,

ik moet volgende functie bespreken:
f(x)=arctan[(x⁴-1)/(2x²)]
dit is mij al helemaal gelukt op enkele details na:
deze functie is continu over R\{0} omdat 0 in de noemer niet kan. hoe noemt dit punt dan? een perforatie ofzo.
verder heb ik de 1ste afgeleide berekend:
f'(x)=4x/(x⁴+1)
der is dus 1 nulpt, nl. x=0, noem ik dit punt voor f(x) een min? want deze bestaat niet in x=0,of noemt dit iets van een imaginair minimum?
dank
sonny
Sonny
Student universiteit België - woensdag 13 december 2006

Antwoord

We weten dat arctan een stijgende functie is.
laten we nu eens kijken naar (x⁴-1)/(2x²)=¹/₂x²-¹/_2x²
Het zal duidelijk zijn dat de limiet hievan voor x nadert tot nul gelijk is aan -¥.
Aangezien lim_x®-¥arctan(x)=-p/2 zal f(x) voor x®0 naderen tot =-p/2, maar deze waarde niet bereiken.
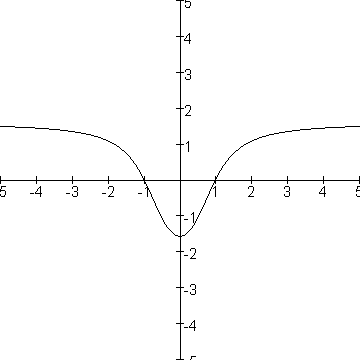
Conclusie: f heeft voor x=0 een perforatie. f heeft geen minimum.
Ter illustratie de grafiek:

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 13 december 2006