WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Integreren, Substitutie, Goniometrie

Beste meneer of mevrouw,

1) Kunt U mij uitleggen hoe ik onderstaande integraal moet uitrekenen?
$\int{}$1/(2+sin(x))dx

In mijn boek staat dat je de speciale substitutie ' y=tan(x/2)' moet gebruiken om de integraal op te lossen. Als je deze substitutie toepast kom je uit op: sin(x)= 2y/(1+y²). Vervolgens is het antwoord op mijn vraag: (2/√3)·arctan((1+2tan(x/2))/√3) + C
Ik ben niet zozeer geïnteresseerd in het antwoord, maar des te meer hoe je via de gegeven substitutie tot dat antwoord komt?

2) Een zelfde soort vraag: hoe bereken je de integraal $\int{}$1/(x·√(x² +1))dx , indien gegeven de substitutie: √(x² + 1) =1/cos(y) en je moet uitkomen op het antwoord: ln(tan(arctan(x))/2) + C

Mijn docent is al lange tijd ziek. Als U mij helpt dank ik U daarvoor hartelijk!
Sara

Saar
Student universiteit - dinsdag 21 november 2006

Antwoord

Beste Sara,

1) Sta me toe de substitutie te schrijven als t = tan(x/2). In principe maakt de naam helemaal niet uit (y mag ook!) maar je zult deze substitutie in de literatuur (ook online) vaak terugvinden als de "t-substitutie". Met deze substitutie kan je een rationale functie van sin(x) en cos(x) steeds omzetten in een rationale functie van t, die op zijn beurt altijd te integreren is.

Het idee is dat je als substitutie t = tan(x/2) neemt, waardoor sin(x), cos(x) en ook dx een rationale functie worden van t, ik verwijs naar deze link voor de resultaten, dit kan je eenvoudig zelf nagaan. We hebben hier:

sin(x) = 2t/(1+t²) en dx = 2/(1+t²) dt

De integraal gaat dus over in:

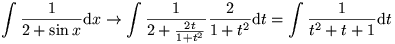
De laatste overgang is het vereenvoudigen van die rationale functie, dat kan je zelf nagaan. Dit kan je nu primitveren, daarna terug t = tan(x/2) substitueren.

2) Bij opgave twee lijkt die susbtitie nu nogal vreemd gekozen, nochtans kan je het logischer aanpakken. Bij vierkantswortels probeer je goniometrische identiteiten uit te buiten en bij bvb vierkantwortels uit 1-x² doen we dat met sin of cos omdat sin²a+cos²a=1.

Hier kunnen we de identiteit 1+tan²a = sec²a gebruiken waar sec(a) = 1/cos(a), de secans. De substitutie is dan veel eleganter zo te schrijven:

Stel x = tan(y) Þ dx = sec²y dy. De integraal gaat dan over in:

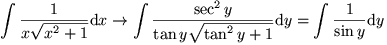
Waarbij de laaste stap opnieuw vereenvoudiging is, dit keer met goniometrie: zelf even na te gaan. Ik vermoed dat de oplossing er wel anders zal uit zien, misschien heb je een foutje doorgegeven: tan(arctan(x)) is immers gewoon x...

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 21 november 2006