WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Oppervlakte wentellichaam

Dit is een reactie op vraag 47370

Dag Anneke,

Dat had ik ook al in gedachten, zou je het ook wat 'wiskundiger' kunnen formuleren of valt dat buiten het bestek van wisfaq?
Integratietheorie (maattheorie, etc) heb ik nog niet gehad maar binnenkort ga ik het wel bestuderen. Zou het daarmee te verklaren zijn of moet ik het elders zoeken?
Jonas
Student universiteit - maandag 30 oktober 2006

Antwoord

Wanneer je het gebied onder de grafiek van een functie gaat wentelen om de x-as kun je dit omwentelingslichaam benaderen met afgeknotte kegels.

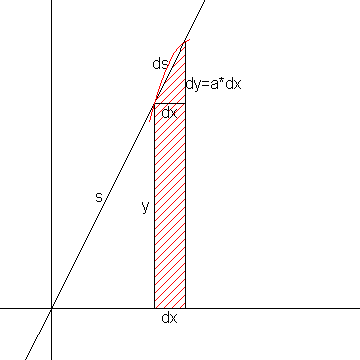
Van zo'n (afgeknotte) kegel kun je een uitslag maken:

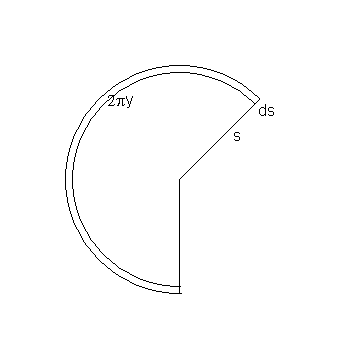
De uitslag van de hele kegel is een cirkelsector met straal s en omtrek 2py
Wanneer je nu x laat toenemen met dx dan neemt de lengte van een beschrijvende van die kegel toe met ds. De straal van deze cirkelsector neemt dan toe met ds.
De "aangroei" is dan 2py·ds.
Wannneer we terug gaan naar de grafiek dan is ds=Ö(dx²+a²·dx)=Ö(1+a²)dx, zodat de totale aangroei gelijk is aan 2pyÖ(1+a²)dx.
De fout die je maakt door te willen benaderen met een cylinder is dat je daar in plaats van het lijnstukje ds ter lengte Ö(1+a²)dx het lijnstukje dx neemt.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 31 oktober 2006