WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Bewijs formule oppervlakte cirkel

Dit is een reactie op vraag 47251

Ik ben benieuwd hoe de primitieve van de integraal van de wortel uit (r in het kwadraat min x in het kwadraat) maal dx eruit ziet en vooral hoe je die primitieve berekent.

Het tweede bewijs begrijp ik niet. Tussen de integratie- grenzen 0 en r bevindt zich toch de halve cirkel? En het ringen verhaal begrijp ik ook niet. Hoezo kun je aannemelijk maken dat je de oppervlakte van een cirkel bepaalt door de integraal van de omtrek van een(halve) cirkel te bepalen?

Robert
Iets anders - maandag 23 oktober 2006

Antwoord

zie plaatje:

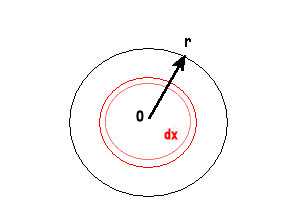
Een cirkel kun je opgebouwd denken uit concentrische cirkels.
1 zo'n cirkel is hier in het rood getekend.
De afstand van deze cirkel tot het middelpunt is x.
De dikte van de cirkel is infinitesimaal klein: dx.
Dan is de oppervlakte van zo'n cirkel (in het infinitesimale geval)gelijk aan 2px.dx

Wanneer we nu de oppervlaktes van al die concentrische ringen sommeren, krijgen we dus de totale oppervlakte van de cirkel.
Daarvoor moet je de integraal nemen van x=0 tot x=r van 2px.dx

ò2px.dx = [px²]^r₀ = pr²

hopelijk is het zo ietsje duidelijker?

groeten,
martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 23 oktober 2006

Re: Re: Bewijs formule oppervlakte cirkel