WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Volume paraboloïde

Goeiedag,

De volgende paraboloïde moet een kom voorstellen waarvan ik de inhoud wil weten:

P: x²-y+z²=0

x gaat van -2 tot +2, z gaat ook van -2 tot +2 en de hoogte y gaat van 0 tot 4.

Ik heb het volume berekend met een enkele integraal (gaat hier perfect) en kom 25.132 uit (heb dit gecontroleerd met een formule dat ik in een wiskunde boek heb gevonden). Nu probeerde ik ook eens dit volume te berekenen mbv een dubbel integraal maar kom niet tot hetzelfde resultaat. Volgens mij moet die integraal er toch zo uitzien:

òò(4-x²-z²)dxdz

waarbij de grenzen voor x en z gaan van -2 tot +2

Deze integraal geeft als uitkomst 21.333 maar ik zie echt niet in waar ik gemist ben bij het opstellen van de integraal.
Benny
Iets anders - dinsdag 3 oktober 2006

Antwoord

y=x²+z²:
Deze paraboloïde ligt dus als t ware op z'n kant, de top 'wijst' vanaf de positieve y-as naar de oorsprong.
Omdat we het volume IN de kom willen weten, is het handiger om de parabool eerst van richting om te klappen: y=-x²-z²
En omdat we weten dat de hoogte van 0 tot 4 ging, verschuiven we de paraboloïde over 4 in de positieve y-richting.
De figuur die je nu hebt laat makkelijker de (betreffende) inhoud berekenen.

y=-x²-z²+4

Nu het integratiegebied.
Je zei dat het gebied omschreven wordt door: x loopt van -2 tot 2 EN z loopt van -2 tot 2. Maar dit klopt volgens mij niet helemaal. Want dit zou betekenen dat het gebied een vierkant is.
Het gebied is echter cirkelvormig: x²+z²=4.
Dit betekent dat x loopt van -Ö(4-z²) tot +Ö(4-z²),
En dat z loopt van -2 tot 2. (x en z zijn in dit verhaal inwisselbaar)
welnu,

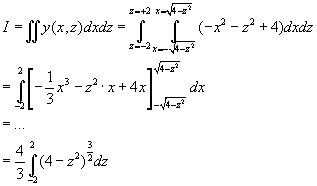
En kijk dan even op http://integrals.wolfram.com wat de primitieve moet zijn.

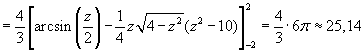
(naschrift: vóór de arcsin in de primitieve moest nog een factor 6 staan. dus 6arcsin(z/2) ..etc)

Dus met de dubbele integraal kom je toch aardig dicht bij je oorspronkelijke resultaat.

groeten,
martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 3 oktober 2006