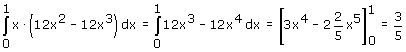WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Verwachtingswaarde

Hallo,

Gegeven is de continue stochastische variabele X met uitkomsten op [0,1] en verdelingsfunctie F: [0,1]®[0,1] waarin F(x) = P(Xx) = 4x³-3x⁴

De verwachtingswaarde E(X) moet van deze functie bepaald worden.

Ik heb in mijn dictaat gelezen dat de verwachtingswaarde voor een continue stochastische variabele met deze formule bepaald kan worden: E(T)=òtF'(t)dt (met de integraal van F over [a,b] interval [a,b] is [0,1])

Tot nu toe ben ik zo ver gekomen: F moet eerst gedifferentieerd worden, dit is: 12x²-12x³. Vervolgens moet het geintegreerd worden, dit is: 4x³-3x⁴. Logisch, want je komt dus gewoon weer op hetzelfde uit. 4x³-3x⁴ moet nu vermenigvuldigd worden met t. t moet ook geintegreerd worden neem ik aan, dit wordt: 1/2t². Ik kreeg: 1/2x²(4x³-3x⁴)dt. Vereenvoudingen: 2x⁵-1,5x⁶. als je het interval [0,1] invult in de gevonden formule, krijg ik er 0,5 uit. In het antwoord staat dat er 3/5 uit moet komen. Wat doe ik fout?

Met vriendelijke groet,
Marion
Student universiteit - maandag 14 augustus 2006

Antwoord

Je rommelt en beetje met je variabele! Het is of 'x' of 't' en niet beide! In je formule staat F' uitgedrukt in t. Je kan 't' gebruiken... maar ik gebruik toch maar 'x'. Je integraal wordt dan:

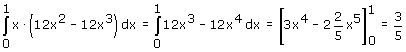
...en dan klopt het allemaal precies lijkt me...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 14 augustus 2006