|
|
|
\require{AMSmath}



Faseverschil
hoe bereken je het faseverschil tussen cos(5x-10) en sin(5x)? en tussen 8cos(2x-4) en 6cos2(x-0.50)?(uitgedrukt in periode)
Inge
Leerling bovenbouw havo-vwo - dinsdag 13 juni 2006
Antwoord
Het faseverschil is de horizontale afstand tussen twee overeenkomstige punten op de beide grafieken (b.v. twee toppen of twee punten waar de grafieken stijgend door de gemiddelde hoogte gaan) gedeeld door de periode.
Bekijken we de grafieken van 8cos(2x-4) en 6cos(2(x-0.50)).
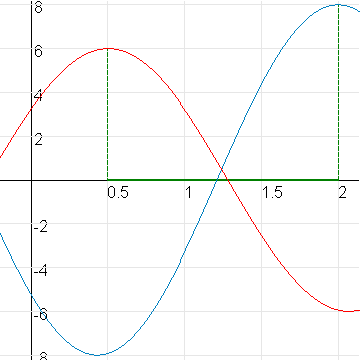
De periode van beide grafieken is 2$\pi$/2=$\pi$.
Het lijkt erop dat de horizontale afstand tussen de toppen van beide grafieken gelijk is aan 1,5.
Dat kan wel kloppen want 8cos(2x-4)=8cos(2(x-2))
Als we dat vergelijken met 6cos(2(x-0.50)) dan is de horizontale afstand tuseen x-0.5 en x-2 gelijk aan 2-0.5=1.5.
Het faseverschil is dan 1,5/$\pi$
Dan de eerste opdracht cos(5x-10) en sin(5x).
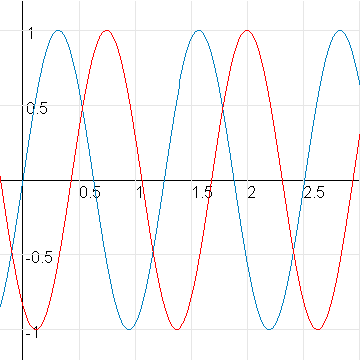
De rode grafiek is de cosinus grafiek, de blauwe de sinusgrafiek.
Omdat cos(5x-10)=cos(5(x-2) heeft deze een top bij x=2.
De periode van beide grafieken is 2$\pi$/5.
De eerste top van de sinusgrafiek ligt bij 0.5$\pi$/5=0.1$\pi$.
De tweede top ligt dan bij 0.1$\pi$+2/5$\pi$=5/10$\pi$=1/2$\pi$.
De afstand tussen de toppen van de rode en de blauwe grafiek is dus 2-1/2$\pi$.
Het faseverschil is dan (2-1/2$\pi$)/(2$\pi$/5)

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 16 juni 2006
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|











