WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Bijzondere koordenvierhoek

In een koordenvierhoek ABCD snijden de diagonalen elkaar loodrecht in het punt S.
K is het midden van CD. KS snijdt AB in L.
Mijn vraag is nu dat hoe moet ik nou bewijzen dat KL loodrecht staat op AB? Wat moet je doen om te bewijzen dat iets loodrecht is?

Stefan
Leerling bovenbouw havo-vwo - vrijdag 19 mei 2006

Antwoord

dag Stefan

Voor dit soort vragen is niet zomaar een kant-en-klaar recept te geven.
Dat is eigenlijk ook wel mooi
Een beetje spelen met hoekensom van een driehoek, hoeken die op een cirkelboog staan, de stelling van Thales: dat zijn de gereedschappen waar je het mee moet doen.

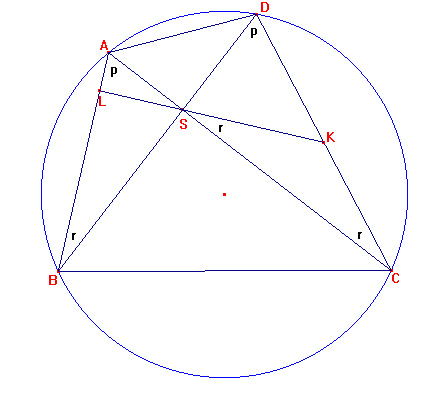
In de bovenstaande figuur geven gelijke letters (p en r) gelijke hoeken aan. Kun je dat voor elk van die hoeken aantonen? Waarom is bijvoorbeeld KS gelijk aan KC (en dus $\angle$KSC = $\angle$KCS)?
Verder geldt:
p+r = 90°
Kom je er dan uit?
succes,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 19 mei 2006