WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Staaf kan net de hoek om

Een gang die 2m breed en 3m hoog is maakt een haakse hoek. Een dunne onbuigzame staaf kan nog net de hoek om in die gang. Wat is op zijn hoogst de lengte van die staaf?

Alweer mij!!
Dit zou het laatste probleem moeten zijn. En alweer heeft de leerkracht mij de moeilijkste gegeven, dus ik kom er weer een niet uit.
Zou jij weer eens zo lief kunnen zijn?????
Trouwens een vraagje! Doe je dit allemaal voor de lol? Omdat je gewoon erg goed bent in wiskunde? Of is dit je werk?

Toedeloe, Ramona
ramona
Student hbo - maandag 30 september 2002

Antwoord

Hoi,

Tuurlijk ben ik zo lief...

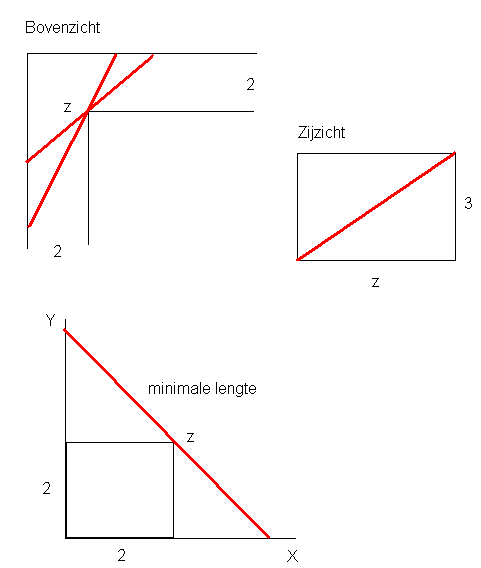
De balk heeft een maximale lengte als ze geplaatst wordt zoals in het zijzicht en de hoek van de gang raakt. Het bovenaanzicht geeft een beperking die de maximale lengte van de horizontale projectie bepaalt. Intuitief zie je dat dit zal zijn met x=y. Je kan het ook berekenen (z uitdrukken ifv x, afgeleide enz). Hieruit bereken je z. Uit het zijaanzicht bereken je dan de maximale lengte van de balk. Dit zijn een paar hints, geen volledige oplossing...

Je leerkracht vindt zijn inspiratie wellicht op http://cage.rug.ac.be/~hvernaev/NWI.html (opgave 46).

Wat je andere vraagje betreft: dit is mijn werk niet en ik word er niet voor betaald... Ergens vind ik er wel lol in, anders zou ik het helemaal niet doen. En daardoor denk/hoop ik dat ik het ook een beetje 'goed' kan. Dit soort probleempjes zijn een soort herhalingsoefeningen voor mij, om alles een beetje up-to-date te houden. In het Latijn zeggen ze: memoria minuitur nisi eam exerceas (het geheugen vermindert als je het niet oefent). Hetzelfde geldt voor wiskunde, wat ook enig geheugenwerk vergt... Dank voor je compliment in ieder geval.

Groetjes,
Johan

andros

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 1 oktober 2002