WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Inhoud balk in kegel

Hallo,
Bereken de maximale inhoud van de balk die past in een KEGEL met als grondvlak een cirkel met straal 6. De hoogte van de kegel is 12,369. Deze cirkel word precies omsloten door een vierkant van 12 bij 12 cm! Teken het grondvlak op ware grootte.

Hoe moet ik deze oplossen a.u.b...?
s
Leerling bovenbouw havo-vwo - vrijdag 5 mei 2006

Antwoord

Eerst maar 's het grondvlak:

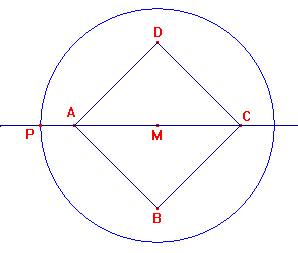
Recht boven A (B, C en D) raakt de balk de kegel.

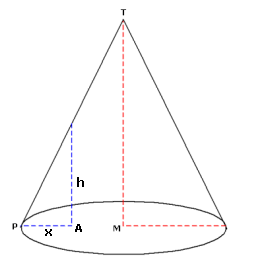
Neem (bijvoorbeeld) x=AP en druk de zijde van het vierkant uit in x en de hoogte h ook in x. De inhoud is dan:

Inh=AB²·h

Je krijgt dan een uitdrukking in x. Maximaliseren dus...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 5 mei 2006