|
|
|
\require{AMSmath}



Afgeleide functie
Wanneer is een limiet van x a gelijk aan + oneindig of - oneindig? a gelijk aan + oneindig of - oneindig?
bv. : lim 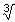 x+1 / x+1 / 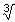 (x-1)^2 = + oneindig (x-1)^2 = + oneindig
x 1 1
Waarom is dit gelijk aan + oneindig?
Elke V
3de graad ASO - donderdag 26 september 2002
Antwoord
Vaak kun je met een beetje "natte-vinger-werk" wel zien wat de limiet gaat worden.
In de teller kun je domweg x = 1 invullen. Dat levert de waarde 1 + 1 = 2 op.
Nu de noemer: als je eerst even probeert of je niet gewoon x = 1 kunt invullen, dan blijkt dat helaas de waarde 0 op te leveren.
Als x vlak bij 1 in de buurt komt, dan is x - 1 bijna gelijk aan 0, maar het kan er nét onder maar ook nét boven zitten.
Omdat je x - 1 nog moet kwadrateren wordt het dus altijd een klein, maar wel positief getal.
Je zit dus met een teller die niet moeilijk doet en gewoon de waarde 2 wil aannemen. Dit getal (bijna) 2 wordt vervolgens gedeeld door een positief getal dat bijna nul is.
Tik nu eens in: 2/0,01 of 2/0,0001 en je ziet dat er gigantische waarden uit gaan komen. Hoe dichter je noemer bij nul komt, des te groter wordt het.
Conclusie: de breuk gaat naar + oneindig.
Als je in dit soort gevallen twijfelt, laat je rekenmachine dan eens een tabel genereren en neem voor x getallen dicht bij 1. Dan zie je alvast wat de resultaten zijn.
MBL
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 26 september 2002
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 a gelijk aan + oneindig of - oneindig?
a gelijk aan + oneindig of - oneindig? 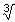 x+1 /
x+1 / 