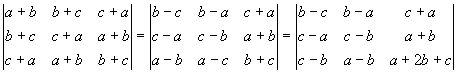WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Oplossen van een derdegraad met 3 onbekenden

Dit is een reactie op vraag 44477

Het gaat daar op verder. De vorige vraag was een deel van de totale vraag, en dit ook. Mijn vorige vraag waar jij mij een tip gaf kwam volledig uit.. En nu is er nog een laatste vraag:
Zijn a,b,c element van R en niet allen gelijk, en is D=0 dan moet a+b+c=0
Concreet moet ik bewijzen dat de oplossing van de vergelijking : a³+b³+c³-3abc =0
a=-b-c is..
Sorry indien ik onduidelijk was.
bedankt voor je snelle reactie
lettor
lettor
3de graad ASO - woensdag 22 maart 2006

Antwoord

Beste Lettor,

Je zou kunnen aantonen dat (a+b+c) een factor is in de ontbinding van die uitdrukking, maar prettig zal dat niet worden. Het lijkt mij trouwens dat je in deze nieuwe opgave dan moet uitgaan van de oorspronkelijke matrix, zonder de a+b+c=0 te gebruiken (dat moet je net aantonen, gebruik maken van D = 0).

In dat geval zou ik terug met de originele matrix beginnen en dan eigenschappen toepassen, op die manier ontbind je de determinant al. Een voorstel:

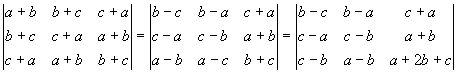
Ik trok eerst van de 1e en 2e kolom de 3e af. Daarna telde ik bij de 3e rij de 2e op. Vergelijk nu eens rij 1 en rij 3. Tel bijvoorbeeld bij rij 3 de 1e rij op, je krijgt dan eerst twee nullen en dan mooi 2(a+b+c). Dat ziet er goed uit, niet?

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 22 maart 2006