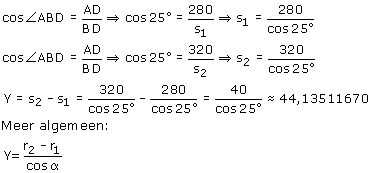WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Verplaatsing in Y van 2 cirkelmiddelpunten op een v-blok bij 2 diameters

Het middelpunt van een as (cirkel) word verplaatst als de cirkel groter/kleiner wordt, en dit op een v-blok waarop de cirkel word ondersteund.

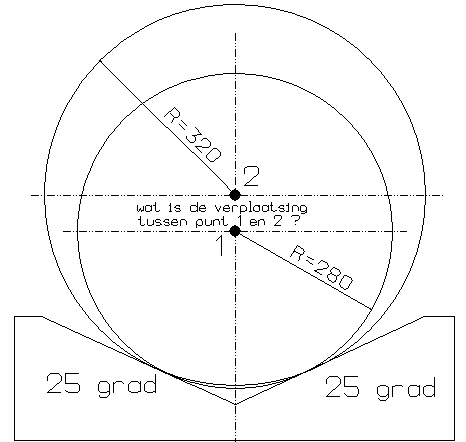
Hoe kan ik met zo weinig mogelijk gegevens in formulevorm erachter komen wat deze verplaatsing is in Y mm?

Een aantal gegevens heb ik bijvoorbeeld; en dat is een as
met een asradius van 280 mm op een V-blok van 25 graden ondersteund(vanuit horizontaal gezien).

Nu vergroot ik de asradius van 280 mm naar 320 mm.

Wat is nu de incrementele middelpuntverplaatsing van de twee cirkels onderling in Y mm?

Ik weet dat het zo'n beetje 44.217 mm in Y moet zijn, maar hier ben ik te gemakkelijk achter gekomen door het geheel in een tekenprogramma te kunnen opmeten. En een formule hiervoor lijkt mij makkelijker!?
twanne
Ouder - maandag 13 maart 2006

Antwoord

Het klonk ingewikkeld, maar met de tekening gaat het lukken. De cirkels raken aan het v-blok. Dat betekent dat de straal loodrecht op het raakpunt staat. Wiskundig gezien heb je dan de situatie:

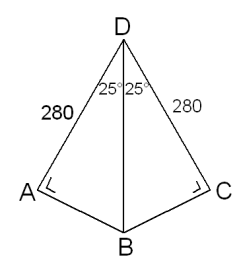
Met de cosinus kan je dan BD uitrekenen. In de tweede situatie verandert er niets, alleen de straal. Dan kan je ook met de cosinus BD uitrekenen. Dus de afstand Y is gelijk aan:

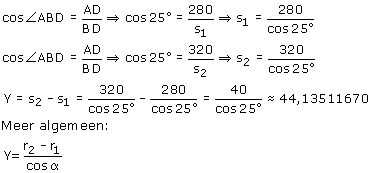
Dus dat valt me reuze mee...
Hopelijk helpt dat.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 17 maart 2006