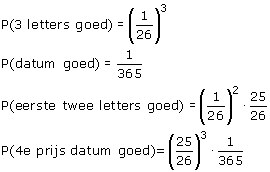|
|
|
\require{AMSmath}



Kansen bij een andere soort loterij
Een loterij waarbij je meespeelt met je favoriete dag als lotnummer. Als je bijvoorbeeld geboren ben op 2 augustus dan doe je mee met de cijfers 0208. Aan deze 4 cijfers voegt de loterij een unieke serie van drie letters toe. Samen vormen zij het lotnummer waarmee je speelt.
Voorbeeld:
25 juni lotnummer RMS 2506
18 november lotnummer KIA 1811
Hoe bepaal je nou hoe groot de kans is dat je iets wint?
Hoe bereken je bijvoorbeeld de kans dat je de hoofdprijs wint of de 2e prijs wint?
- Hoofdprijs Letters + datum goed
- Troostprijs Eerste 2 letters + datum van hoofdprijs goed
- Troostprijs Eerste letter + datum van hoofdprijs goed
- Troostprijs Alleen datum van hoofdprijs goed
- 1ePrijs Letters + datum goed
- 2ePrijs Eerste 2 letters + datum goed
- 3ePrijs Eerste letter + datum goed
- 4ePrijs Datum goed
- 5ePrijs Maand goed
- 6ePrijs Dag goed
Chris
Leerling bovenbouw havo-vwo - maandag 13 februari 2006
Antwoord
Als je vraagt 'wat is de kans dat je iets wint' is dat dan met de 2 genoemde loten? Of bij 1 lot? En hoe stel je je dat voor? Volgens mij moet je alle afzonderlijke kansen op de verschillende prijzen berekenen. Dat gaan we niet doen... Spelregels niet gelezen?
Om je op weg te helpen:
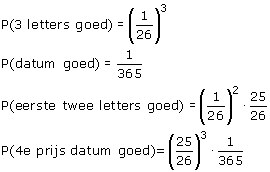
De rest gaat precies zo, maar dan anders...
Ik heb maar even niet gelet op schrikkeljaren, maar dat kan je natuurlijk ook nog doen... Overigens is de vraag eigenlijk niet helemaal duidelijk! Wordt de 'favoriete dag' willekeurig getrokken of op basis van de uitgedeelde loten? Worden voor de lettercode alle codes 'willekeurig' uitgedeeld? En heeft elke code dezelfde kans? Vragen, vragen, vragen...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 14 februari 2006
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|