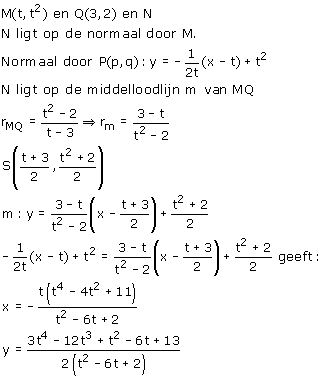|
|
|
\require{AMSmath}



Conflictlijn parabool-punt
Hoe construeer je een conflictlijn tussen een parabool en een punt (dat buiten de parabool ligt)? En heeft deze conflictlijn een naam?
Erick
Leerling bovenbouw havo-vwo - woensdag 8 februari 2006
Antwoord
Leuk hoor...
In Cabri is de constructie van isoafstandslijn nog wel te doen. Hieronder zie je 't resultaat.
Applet werkt niet meer.
Download het bestand.
Je kunt 'X' verslepen.
Om 't een beetje toe te lichten. De punten van de isoafstandslijn liggen op de normaal in M van de parabool en op de middelloodlijn van MQ. In dat geval kan je misschien 'de vergelijking' voor de kromme ook wel bepalen. Ik heb dat 's gedaan voor y=x2 en Q(3,2).
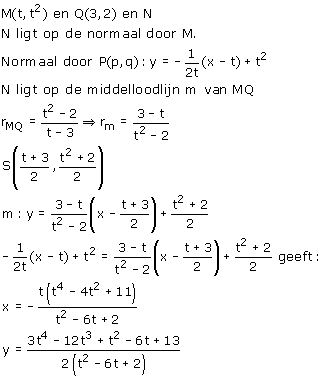
Als je dat tekent dan lijkt me dat wel aardig te kloppen allemaal:
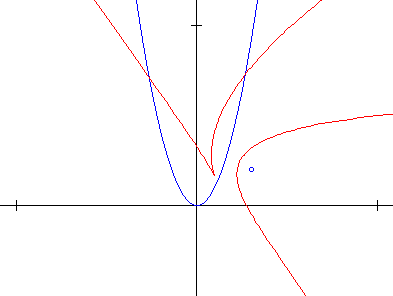
Maar ja... is dat nu een 'bekende' kromme? En zou je er verder nog iets leuks mee kunnen? Ik weet het niet, ik vond 't zo wel mooi al...
Aardig is nog wel om Q binnen de parabool te kiezen. Q laten samenvallen met het brandpunt van de parabool is ook vast leuk... je kunt je afvragen welk punt M het 'keerpunt' bepaalt van de meetkundige plaats... en wat allemaal niet meer?
Hopelijk heb je er wat aan...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 13 februari 2006
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|