WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

3 kegels in 1 cilinder

Hoe kan aangetoond worden dat de inhoud van een kegel met een rond grondopp ¹/₃ deel is van de inhoud van de cilinder met het zelfde grondopp en hoogte?

Ik weet dat de inhoud van een cilinder grondopp · hoogte is
en de inhoud van een kegel ¹/₃ · grondopp · hoogte
maar hoe kom ik kan ik aantonen dat dit ¹/₃ deel is?
Henk
Leerling bovenbouw havo-vwo - donderdag 19 januari 2006

Antwoord

Dag Henk

Als je hebt gewerkt met integralen weet je dat de inhoud van lichaam, dat verkregen wordt door het wentelen rond de x-as van een functie f(x) tussen de grenzen x=a en x=b gelijk is aan
$\pi\int{}$f²(x).dx tussen de grenzen a en b.
Een cilinder met straal r en hoogte h krijg je door de rechte y=r, begrensd tussen x=0 en x=h te wentelen rond de x-as.
De inhoud van dit cilinder vind je door:
$\pi\int{}$r².dx tussen de grenzen o en h = $\pi$.r².h

Een kegel met straal r en hoogte h krijg je door de rechte y=^r/_h.x, begrensd tussen x=0 en x=h te wentelen rond de x-as.
De inhoud van deze kegel vind je door:
$\pi\int{}$(^r/_h)².x².dx tussen de grenzen o en h =
$\pi$.^r²/_h².¹/₃.h³ = ¹/₃$\pi$r².h

Om dit meetkundig aan te tonen kun je beginnen met aan te tonen dat de inhoud van driezijdig piramide gelijk is aan één derde van de inhoud van een driezijdig prisma met hetzelfde grondvlak en dezelfde hoogte.
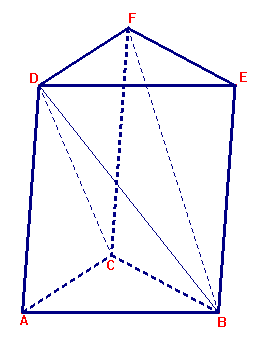
Het prisma (ABC,DEF) (zie beneden) kun je verdelen in een driezijdig piramide P₁=(D,ABC) en een vierzijdig piramide (D,CBEF).
Dit vierzijdig piramide kun je weer verdelen in een driezijdig piramide P₂=(D,CBF) en het driezijdig piramide P₃=(D,BEF).

Deze laatste twee piramides P₂ en P₃ hebben dezelfde inhoud want de oppervlakte van hun grondvlakken en hun hoogtes zijn gelijk.

Het piramide P₃=(D,BEF) kun je ook bekijken als het piramide (B,DEF), dus met B als top en DEF als grondvlak. Dan kun je zien dat de piramides P₁ en P₃ dezelfde inhoud hebben want oppervlakte van hun grondvlakken en hun hoogtes zijn gelijk.

Dus de inhouden van de drie piramides zijn precies gelijk, zodat de inhoud van P₁ gelijk is aan één derde van de inhoud van het gehele prisma.

Deze regel geldt ook voor meerzijdige prisma's en piramides want deze kun je steeds beschouwen als een samenvoeging van driezijdige prisma's en piramides.

En een cilinder en kegel kun je beschouwen als een limiettoestand van regelmatig prisma en piramide.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 19 januari 2006