WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hyperbool, een raaklijn en een lijn loodrecht

We komen er weer niet uit...

Gegeven is de hyperbool x²-y²=1
In een veranderlijk punt R van deze hyperbool wordt de raaklijn getekend. Deze raaklijn snijdt de y-as in een punt P. Door R wordt ook de lijn loodrecht op de raaklijn getekend. Deze laatste snijdt de y-as in Q Bewijs dat OP·OQ constant is.

We hebben de hyperbool getekend en allerlei raaklijnen met bijbehorende loodlijnen. Wat bedoelen ze nu eigenlijk met constant? Dat het antwoord constant (met dezelfde factor)vergroot? Het lijkt in eerste instantie allemaal niet zo moeilijk, maar dat bewijzen blijft lastig...

Bij voorbaat dank voor de hulp!
jurjen
Leerling bovenbouw havo-vwo - vrijdag 6 januari 2006

Antwoord

Eerst maar 's een tekening:

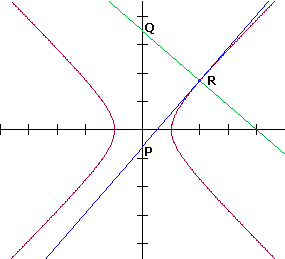
Als je nu voor R(p,Ö(p²-1)) neemt (deze punten liggen boven de x-as) dan kan je een algemene vergelijking voor de raaklijn aan de hyperbool in R opstellen. Het wordt iets van de vorm y=...·x+b. Hierbij staat er op de puntjes een uitdrukking in p. Als je dan de coördinaten van R invult kan je b uitdrukken in p.

Hetzelfde kan je doen voor de lijn loodrecht op de raaklijn. Je krijgt dan iets van de vorm y=...·x+c. Na invullen van de coördinaten van R kan je c uitdrukken in p.

En o wonder boven wonder als je dan b·c berekent komt daar gewoon -2 uit... waarmee aangetoond is dat OP·OQ constant is (voor de punten boven de x-as). Best leuk om te doen..., maar probeer het maar eens. Mocht het niet lukken, dan horen we 't wel...

P.S.
Als ik daar nu zo 's over nadenk dan had je dit wellicht zelf ook kunnen bedenken als je bijvoorbeeld het 'hele verhaal' eens zou doen voor een concreet geval (bijvoorbeeld voor R(2,Ö3)). Als je dat kan kan je 't ook voor het algemene geval... althans dat zou dat in ieder geval richting kunnen geven waar je de oplossing zou kunnen vinden.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 6 januari 2006