WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Bewijs integratieregels

Hoe komt men tot de regel dat de bepaalde integraal over het interval [a,b] van f(x) die overal continu is in het interval [a,b] gelijk is aan het tegengestelde van de integraal over het interval [b,a]?
Gery
3de graad ASO - zondag 25 december 2005

Antwoord

Beste Gery,

Voor notaties met intervallen nemen we conventioneel eerst de kleinere waarde en dan de grotere. In de veronderstelling dat a b spreken we dus wel van [a,b] maar niet van [b,a]. Wat je waarschijnlijk bedoelt is dat het wisselen van de integratiegrenzen het teken verandert.

Nu zou je kunnen teruggaan naar de definitie van de integraal, maar de manier waarop deze ingevoerd en gedefinieerd wordt is afhankelijk van bron tot bron. Het kan dus afhangen van de keuze van de auteur, maar het resultaat is steeds hetzelfde. Gewoonlijk werk je met een partitie waarbij het wisselen van de grenzen resulteert in een tekenwisseling van elk deelinterval.
Soms wordt dit ook wel als rekenregel gewoon per definitie gesteld, net zoals de integraal van a tot a gelijkgesteld kan worden aan 0.

Om te zien dat dit een zinvolle keuze is kan je kijken naar de grondformule van de integraalrekening, daaruit kan je dan afleiden dat:

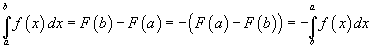
mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 25 december 2005