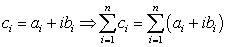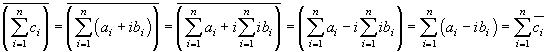|
|
|
\require{AMSmath}
Re: Toegevoegde complexe getallen
Kunt U dat laatste eens demonstreren, aub?(sommatieteken)
Groeten
lemmen
Iets anders - donderdag 15 december 2005
Antwoord
Beste Rik,
Het idee bestaat er in, net zoals in mijn eerder voorbeeld, om de som van de complexe getallen zodanig te herschrijven dat we terug één complex getal hebben (de optelling in C is namelijk inwendig) - met als reëel deel de som van alle reële delen en analoog voor de imaginaire delen. Dan heb je weer een enkel complex getal waarvan je de toegevoegde kan bepalen, daarna 'splits' je terug op in de aparte complexe getallen om vast te stellen dat je van de oorspronkelijk complexe getallen afzonderlijk de toegevoegde kon nemen.
We schrijven dus
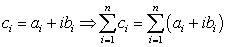
Dan is het spelen met sommaties
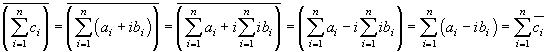
Nu hebben we aangetoond dat complexe toevoeging distributief is over de optelling.
NB: de overlijning staat hier voor complexe toevoeging.
mvg,
Tom
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 15 december 2005
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 42274