WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Bewijs met arctan en pi

Te bewijzen: arctan 1 + arctan 2 + arctan 3 = pi

Het is me dus absoluut onduidelijk hoe ik dit moet bewijzen. Ik ben wel in het bezit van de typische tekening die een rechte lijn vormt, maar verder raak ik niet. Kan iemand me het bewijs uitleggen?
Bruno
3de graad ASO - zaterdag 3 december 2005

Antwoord

Beste Bruno,

Neem bijvoorbeeld eens de tangens van beide leden. Tan(p) is 0 dus je verwacht dat de tangens van het linkerlid ook 0 wordt.

Je kan daarvoor gebruik maken van:

tan(x+y) = (tan(x)+tan(y))/(1-tan(x)tan(y))

Uiteraard gebruik je ook (en dit vereenvoudigt de hele formule en uitwerking aardig!) dat tan(arctan(x)) = x.

Welke 'typische tekening' je bedoelt weet ik niet zeker, maar zie hier een grafische oplossing aangereikt door collega dk.

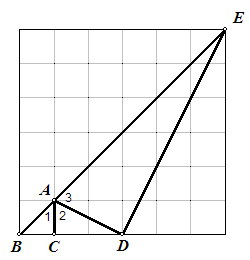
Ga uit van het grote vierkant. De hoeken 1, 2, 3 bij A samen zijn 180° met opvolgend arctan(A₁) = 1, arctan(A₂) = 2, arctan(A₃) = 3.

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 3 december 2005