WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Vraagstukken tweedegraadsvergelijking

Ik help momenteel een meisje met wisunde, maar ondervind problemen met het oplossen van vraagstukken. Meer bepaald bij het opstellen van de vergelijkingen. Kunnen julie me aub volgende zaken uitleggen, ik zou er enorm mee vooruit geholpen zijn:
Er dient een stuk land afgezet te worden met gaas. Er is 60 meter gaas beschikbaar. Wat is de grootst mogelijke oppervlakte die kan afgezet worden? (er hoort een tekening bij, maar ik probeer het uit te leggen: er is een stuk Y, een stuk X en een stuk X-4 dat afgezet dient te worden, aangezien de rest water is). : ik geraak er niet wijs uit.

Bij een gegeven punt van een rechte en een gegeven vergelijking wordt er naar de raaklijnen gevraagd. (vb: y=x²-2x en P(1,-4). Hoe moet dit opgelost worden?

De som van drie getallen is 20 en het eerste getal is gelijk aan de som van de andere twee. Bepaal de drie getallen zodanig dat de som van hun kwadraten zo klein mogelijk is. Ik geraak aan a+b+c=20 en a= b+c. Maar hoe stel je iets op zodat de som van de kwadraten zo klein mogelijk is?

Twee kangaroes zijn aan het springen. Hun sprongen zijn parabolisch van vorm. De eerste springt 4 meter ver en bevindt zich over een afstand van 2 meter hoger dan 75 cm. Hoe hoog springt deze kangaroe? De tweede springt 75 cm hoog en bevindt zich over een afstand van 1,8 meter hoger dan 48 cm. Hoe ver springt deze kangaroe?

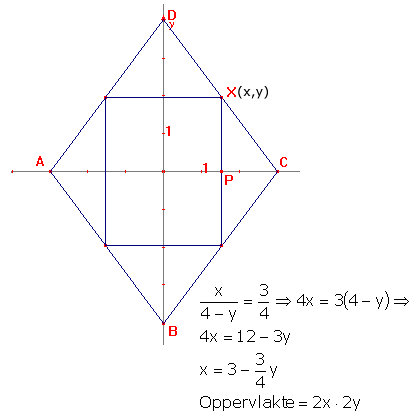
Op elk van de zijden van een ruit met lengte van de diagonalen 6 en 8 nemen we een punt, zodanig dat de verkregen 4 punten de hoekpunten zijn van een rechthoek waarvan de zijden evenwijdig zijn met de diagonalen van de ruit. Bepaal de afmetingen van de rechthoek zodanig dat zijn opppervlakte een maximum bereikt. (kan er niet aan beginnen + ik weet niet hoe je dat maximum moet berekenen)

Om veiligheidsredenen wil een ondernemer een stuk grond omheinen. Hij beschikt hiervoor over een budget van 600 euro. Het stuk grond paalt aan een gebouw dat aan 1 zijde als afsluiting dient. De afsluiting parallel aan het gebow kost 7,5 euro/meter en de afsluiting van de 2 andere zijden kost 5 euro/meter. Welke lengte en breedte moet de ondernemer voor het stuk grond nemen om een maximale oppervlakte te hebben. Hoe groot is deze oppervlakte?

Shadia
Iets anders - zaterdag 22 oktober 2005

Antwoord

HINTS
Mits het gaat om een rechthoekig stuk land. Voor de omtrek geldt:
2x+y-4=60. Hiermee kan je y uitdrukken in x. Als je dan een formule maakt voor de oppervlakte... in x dan kan je die functie maximaliseren.
Misschien heb je iets aan Raaklijnen zonder afgeleide...
a+b+c=20 en a=b+c levert 2b+2c=20 of b+c=10, dus b=10-c. a=b+c levert dan a=10. Eigenlijk ben je er dan al... vanwege de symmetrie... maar als je per se wil kan je ook proberen a²+b²+c² te minimaliseren. Dat is dan 10²+(10-c)²+c².
Maak een tekening. De volgende punten liggen op de eerste parabool:
(-2,0),(-1,³/₄),(1,³/₄) en (2,0).
Bepaal hiermee het functievoorschrift.
De volgende punten liggen op de tweede parabool:
(-.9,.48),(0,.75) en (.9,.48).
Bepaal hiermee het functievoorschrift en de nulpunten.

Je hebt in ieder geval het verband tussen y (de kant parallel aan het gebouw) en x. Er geldt:
y·7,5+2x·5=600.
Je kunt dan de oppervlakte uitdrukken in x en maximaliseren.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 22 oktober 2005