WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Compas koers

Geachte heer/mevrouw,
Ik zit met een opgave die ik wiskundig niet kan beredeneren. de vraag is : een piloot vliegt 20 kilometer in noordelijke richting naar punt a daarna 20 kilometer in westelijke richting tot punt b, wat is zijn compas koers om terug naar het vertrek punt te gaan . nu ben ik met een graden boog in de weer geweest en bij benadering kom ik aan 110/120 graden. Ik weet niet of het goed is en zie er nog geen logica in .
Zou u me alstublieft kunnen helpen.
met vriendelijk groet,
Alexander Cath
A. Cat
Iets anders - donderdag 22 augustus 2002

Antwoord

Beste Alexander,

de opgave zoals ik het begrijp zou de volgende figuur moeten opleveren.

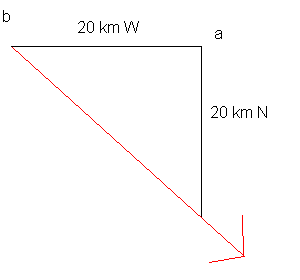
Eerst vlieg je 2 km naar het noorden, om vervolgens 2 km naar het westen te vliegen, daarna moet je terug naar het oorspronkelijk punt. Deze vlucht creëert het patroon van een driehoek. Omdat je in punt a van N naar W gaat, maak je een rechte hoek. Ook zijn de 2 aanliggende zijden van deze rechte hoek gelijk (2 km). Dit betekent dat het een gelijkbenige rechthoek is, wat de oplossing sterk vereenvoudigt.

Bij een gelijkbenige rechthoek zijn de basiszijden gelijk (punt b en het startpunt). De som van de hoeken van een driehoek zijn samen 180°. Van hoek a weten we dat deze 90° is. Dus de 2 overige hoeken zijn samen ook 90°, of elk 45°.

Logisch gezien komt het erop neer dat het vliegtuig 2 km naar het zuiden vliegt en 2 km naar het oosten om in hetzelfde punt terecht te komen. Door de korste weg te nemen, vlieg je perfect richting zuidoosten (dit komt doordat beide zijden gelijk zijn).

Ook wiskundig kom je op zuidoosten: het lijnstuk [ba] ligt op 90° vanop het magnetisch noorden en van daaruit volg je een hoek van 45° (zie eerder) wat een koersrichting van 90+45= 135° geeft. Dit is ook het zuidoosten.

Je komt een iets lagere waarde uit. Dit komt misschien doordat je de beide zijden niet evenlang getekend hebt en/of geen rechte hoek hebt van 90°. Want in dat geval is hoek a geen 45° meer.

Wanneer je geen gelijkbenige rechthoek hebt, kan je het toch nog berekenen. Ik zal deze methode even uitleggen en toepassen op het voorbeeld om te bewijzen dat je terug op 45° uitkomt voor hoek a.

Hiervoor hebben we eerst de stelling van Pythagoras nodig. Deze stelt dat de 2 zijden aan de rechte hoek in het kwadraat gelijk zijn aan de schuine zijde in het kwadraat. OF:
schuine zijde (naar het beginpunt)²=2²km+2²km
schuine zijde²=4+4
schuine zijde²=8
schuine zijde=2,2884

Nu hebben we sinussen en cosinussen nodig.
sin a = overstaande zijde / schuine zijde
sin a = 2 / 2,2884
sin a = 0,7071 (ik heb meerdere cijfers na de komma gebruikt)
a = secans 0,7071
a = 45°

Wat terug het eerdere resultaat geeft als proef.
Zie Goniometrie

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 23 augustus 2002