WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hoe bereken ik een 45 graden pijp

Als ik een loden pijp heb en deze op 45 graden geknipt, daarna door midden dan krijg ik een uitslag. Hoe bereken ik deze?
bijvoorbaat dank
akke v
Iets anders - dinsdag 20 augustus 2002

Antwoord

Laten we eens een pijp nemen met een doorsnede van 10 cm en deze op 4 cm hoogte schuin omhoog (45°) afsnijden.

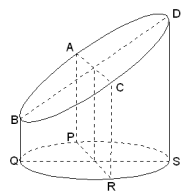
In bovenstaande tekening is QS=PR=10, BQ=4. In dat geval is DS=14 en DB=10√2 en AC=10, zodat we de lengte van de assen van de ellips (bovenvlak) kennen.

Als de figuur nu 'openknippen' langs DS krijgen we een soort uitslag als:

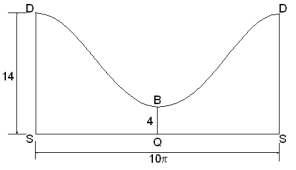
De vraag is nu natuurlijk wat voor een soort kromme DBD is. Stel je voor dat het gewoon een (co)sinus is, dan zijn we gauw klaar..., maar ja is dat zo?

Laten we door QS de x-as aanbrengen, door PR de y-as en precies door het midden de z-as. Voor de cilinder geldt:
x=5·cos(u)
y=5·sin(u)
met u$\in$[0,2$\pi$>

Dit gaan we snijden met een vlak:
z=x+9

Dit levert een parametrisering van de ellips van het bovenvlak:
x=5·cos(u)
y=5·sin(u)
z=5·cos(u)+9
Hierbij 'loopt' u van 0 tot 2$\pi$, waarbij z dus varieert van 4 tot 14.

De vraag is nu: kunnen we z uitdrukken in de 'afgelegde weg' op de cirkel. In dit geval is u de hoek, dus na u graden is de afgelegde weg 5u.
Dus je kunt deze 'functie' van de hoogte opvatten als:
f:5u$\to$5·cos(u)+9

Nemen we in plaats van 5u gewoon x dan is:
x=5u
u=¹/₅·x
f(x)=5·cos(¹/₅·x)+9

Conclusie: inderdaad die kromme DBD is een cosinus.

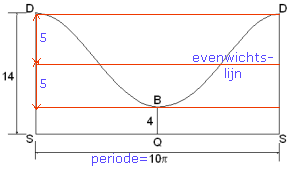
Op hoogte 9 vinden we de evenwichtslijn, de amplitude is 5 en de periode is 10$\pi$.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 21 augustus 2002

Re: Hoe bereken ik een 45 graden pijp