|
|
|
\require{AMSmath}



Wat is een richtingshoek?
Opgave: Bepaal telkens de hoek die de x-as maakt met de gegeven rechte.
Oefening 1: u : y=-2x
oefening 2: z : 3x+4y+2=0
Ik denk dat ik bij de eerste oefening gewoon van het getal sinus of de cosinus moet nemen. Om dan zo het getal in graden, minuten en seconden moet omzetten.
Ik denk bij de tweede oefening dat ik de vergelijking moet omzetten. Naar de volgende vorm y=ax2+b+c en dan zo een sinus, of een cosinus te berekenen. Omdan die uitkomst om te zetten in graden, minuten en seconden.
Jan
Iets anders - maandag 19 augustus 2002
Antwoord
De tangens van de hoek die een lijn (eerstegraads functie) maakt met het positieve deel van de x-as is gelijk aan de richtingscoŽfficiŽnt.
rico = tan $\alpha$
met $\alpha$: de hoek die de lijn maakt met het positieve deel van de x-as.
Oef.1
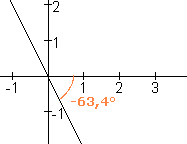 de rico is -2 de rico is -2
tan $\alpha$ = -2
$\alpha\approx$-63,4į
Oef.2
3x+4y+2=0 kan je 'omschrijven' naar:
4y=-3x-2
y=-3/4x-1/2
tan b = -3/4
b$\approx$-36,9į
Voor het omzetten van graden naar graden, minuten en seconden zit er vast een handig knopje op je rekenmachine.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 19 augustus 2002
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








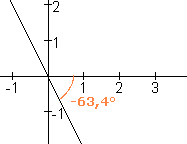 de rico is -2
de rico is -2
