 |
De digitale vraagbaak voor het wiskundeonderwijshome | vandaag | gisteren | bijzonder | gastenboek | wie is wie? | verhalen | contact |
|||||||||||||||||||
|
\require{AMSmath}



Korter schrijven of haakjes wegwerkenIk ben verschrikkelijk slecht in wiskunde en heb maandag een herexamen. Eén van de oefeningen die ik al niet begrijp is de volgende: AntwoordLaten we maar eens kijken wat dit allemaal is.



home | vandaag | bijzonder | gastenboek | statistieken | wie is wie? | verhalen | colofon ©2001-2024 WisFaq - versie 3
| |||||||||||||||||||

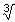 x2·5Öx3/
x2·5Öx3/




 a
a 
