WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Constructie ellips en hyperbool

Hoi,
Ik zoek naar een constructiemethode met passer en liniaal van de ellips en de hyperbool als de halve assen gegeven zijn. Hoe ga ik tewerk?
Ik ken natuurlijk wel de standaardvergelijkingen.
Ellips: x²/a² +y²/b² = 1 waarbij c = √(a²-b²)
Hyperbool: x²/a² -y²/b² = 1 waarbij c = √(a²+b²)
Gezien ik weet dat de halve assen a en b zijn, kan ik vandaaruit de vergelijking verder opstellen en dan de constructie uitvoeren via de coordinaten, maar is er een andere methode?
Hartelijk dank.
Elia
3de graad ASO - dinsdag 7 juni 2005

Antwoord

Voor de ellips verwijs ik naar onderstaande link, en wel de punten 2 en 3 in het aldaar staande overzicht.

Voor de hyperbool gaat eea. min of meer op dezelfde manier, alleen gebruik je nu de volgende identiteit:

sec²$\phi$ - tan²$\phi$ = 1

Hieronder staan twee figuren die daarop betrekking hebben.

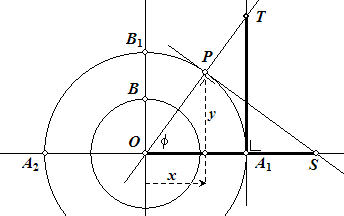
P is een willekeurig punt op de cirkel met straal a en middelpunt O (en OB = b).
In de eerste figuur is OS = a·sec$\phi$ en A₁T = a·tan$\phi$.
waarbij a dus de lengte van de hoofdas is van de hyperbool.
Je moet dan nog een vermenigvuldiging toepassen op A₁T, zodat je een lijnstuk krijgt dat gelijk is aan b·tan$\phi$; dat is de y-coördinaat van het punt X op de hyperbool.
De x-coördinaat van het punt X op de hyperbool is gelijk aan OS = a·sec$\phi$.
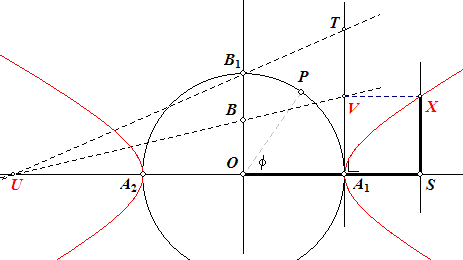
Die vermenigvuldiging geschiedt met de lijnen TB₁U en UBV.
Met VX (// OS) wordt de positie van X (op de loodlijn in S op OS) van de hyperbool bepaald.
Dat laatste staat in de tweede figuur.
Als nu P de cirkel doorloopt, dan doorloopt X de hyperbool met vergelijking
x²/a² - y²/b² = 1

Ik hoop dat je hieraan voldoende hebt.
Ik merk nog wel op dat je op deze manier een ellips en een hyperbool met passer en liniaal slechts punt voor punt kunt construeren!
Zie Ellips-constructies met Cabri

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 9 juni 2005