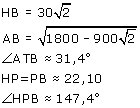WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Verstek van dakplaten van een achthoekige kooi

Ik heb een achthoekige kooi gemaakt. Het probleem is het dak: dat is 30 cm hoog nu heb 8 driehoeken deze komen bij elkaar in de top. De maten van de vogelkooi: de diameter is 60 cm en de hoogte van het dak is 30 cm. De vraag is hoe bereken ik het verstek van de 2 driehoeken die bij elkaar komen kun u mij een voorbeeld geven?
Groetjes.
peter
Student universiteit - zondag 5 juni 2005

Antwoord

Eerst maar een tekening:

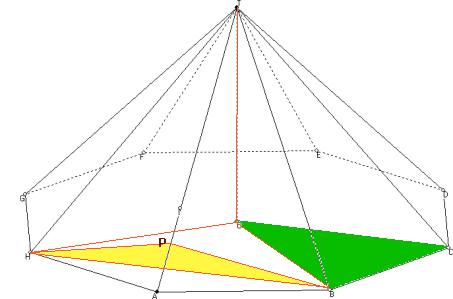
De 'straal' van de achthoek is 30 en de hoogte van de piramide is ook 30. Het gaat nu om de hoek HPB, waarbij HP en PB loodrecht op AT staan. De lengte van HB is 30Ö2, dat is niet het probleem. Maar hoe lang zijn HP en PB?

Als ik die namelijk weet kan je met de cosinusregel de hoek HPB wel berekenen, dus... we gaan op zoek naar de lengte van HP en PB.

In de groene driehoek kan je met de cosinusregel de lengte van BC (=AB) berekenen. AB22,96. In driehoek ABT kan je dan met de cosinusregel de hoek ATB berekenen, deze is ongeveer 31,4°.

Dan kan je met de sinus de lengte van PB berekenen, PB22,10 en dan zijn we er zo'n beetje...

Met de cosinusregel bereken je ÐHPB147,4° en dan weet je de verstekhoek ook. Hopelijk heb ik verder geen rekenfouten gemaakt, want 'echt lollig' is het allemaal niet. Misschien dat ik morgen het antwoord nog even controleer, maar ik kan nu geen vogelkooi meer zien...

Samengevat:

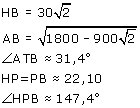
Hopelijk kan je er iets mee...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 10 juni 2005