|
|
|
\require{AMSmath}



Trekking zonder terugleggen
Hallo,
Ik zit een beetje in de knoei:
Het gaat om een vijver met 5 rode, 3 gele en 4 blauwe vissen... Ik haal er drie uit (en doe ze niet terug) Hoe groot is de kans dat de tweede geel is (de eerste en derde vis mogen dus van alles zijn).
Kunnen jullie me helpen?
Alvast bedankt,
Marc H
Leerling bovenbouw havo-vwo - donderdag 2 juni 2005
Antwoord
Het vaasmodel: je hebt een vaas met 12 knikkers waarvan 3 geel (G) en 9 rood (R). Ik haal er 3 knikkers uit, zonder terugleggen. Bereken P(...,G,...). We onderscheiden nu 4 gevallen... Voor deze 4 gevallen kan je de kans uitrekenen, tel ze op en je weet het!
P(G,G,G)=3/122/111/10
P(G,G,R)=3/122/119/10
P(R,G,G)=9/123/112/10
P(R,G,R)=9/123/118/10
Of ietsje handiger opgeschreven: 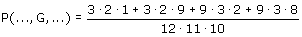
Ik weet zeker dat dit klopt! Maar is het handig?
Anders
Je kunt ook zeggen de eerste knikker is geel of rood, daarna moet je een gele pakken en derde knikker doet er niet toe....
Er zijn twee gevallen:
P(G,G)=3/122/11
P(R,G)=9/123/11
Dus: P(de tweede is geel)=P(G,G)+P(R,G)
Nog anders...
Zou 't uitmaken of je nu eerst de 'eerste knikker' uitkiest of dat je eerst de 'tweede knikker' uitkiest? Of laat ik het anders zeggen... je hebt 3 bakjes en je moet knikkers uit die vaas kiezen die je in die bakjes legt. Zou de kans dat er in het tweede bakje een gele knikker zit veranderen als je eerst willekeurig een knikker kiest en dat in het tweede bakje doet en dan de knikker voor bakje 1 of bakje 3 kiest of........ dat je 't op volgorde doet?
Het antwoord zou moeten zijn: dat maakt niks uit!
P(de tweede is geel)=3/12
...en dat laatste is dan wel het handigst.
Zie ook Wie trekt er aan het kortste eind?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 2 juni 2005
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|