WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Snijpunt tussen een lineaire en exponentiële functie bepalen

In een kostencalculatie geeft Excel me de volgende twee trendlijnen:
y = 46961*X ^(0,3353)
y = 1149,3*X + 24002
Ik wil graag het snijpunt tussen deze twee functies weten. Op basis van de grafiek die ik heb getekend, weet ik dat y rond 300.000 moet liggen, maar alleen een schatting is bij dit vraagstuk niet genoeg. Alvast bedankt!
Annema
Student hbo - donderdag 2 juni 2005

Antwoord

Je zoekt dus een oplossing van de vergelijking:

46961*X ^(0,3353)= 1149,3*X + 24002

Deze vergelijking is niet exact oplosbaar. Je zal het dus wel met een schatting moeten stellen. Als je wat van numerieke analyse kent kan je iteraties opstellen die convergeren naar de oplossing.
bijvoorbeeld een eenvoudige:
f=x-> 40.86052380*x^0.3353-20.88401636

neem een startwaarde dicht bij 230, de geschatte x-waarde voor het verste snijpunt, en doe telkens de iteratie x_n=f(x_n-1)
met x₀=230

Na 17 iteraties kom je tot een stabiel antwoord tot op 7 cijfers na de komma:
x₁₇=233.4083790

(door deze x-waarde in te vullen in één van de vergelijkingen krijg je een benaderde waarde voor y)

Deze iteratie convergeert echter niet naar het eerste snijpunt.

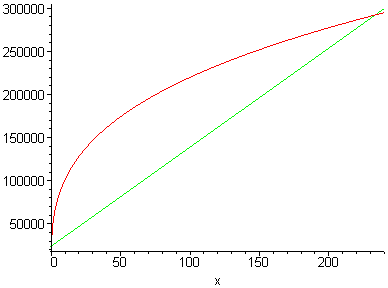
Je ziet dat er twee snijpunten zullen zijn.

Het antwoord voor het kleinste snijpunt is benaderd
x=0.137777

Koen

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 2 juni 2005