WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Via omtrek straal berekenen

Ik zat me eens af te vragen of het mogelijk is de straal en diameter van een cirkel te berekenen als je slechts de omtrek weet. Ik heb toen (volgens mijn eigen berekeningen) het antwoord gevonden: ja.
Nu zou ik het op prijs stellen als een van jullie mijn berekening even nagaat omdat er enkele punten zijn die ik met wantrouw heb uitgevoerd.

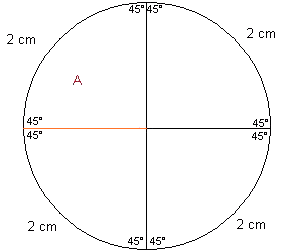De berekening:
Zoals u ziet op het plaatje heb ik als voorbeeld genomen:
Omtrek = 8 cm
Dit betekent dat alle 'c-zijdes' (volgens de stelling van pythagoras) 2 cm zijn. Ik weet dat er 8 hoeken zijn van 45° dus kan ik met goniometrische functies berekenen wat dus die andere twee zijdes zijn. Ik neem driehoek A (aangegeven met rode A) en wil de rode lijn berekenen (dat is de straal van de cirkel):
cos45° = (rood/2)
rood = cos45°*2 1,41

Ik had nog een andere manier:
de driehoek is gelijkbenig dus als zijdes A en B (volgens de stelling van pyhtagoras) even beide x worden genoemd, dan: (x²+x²) = 2 x² = 2
dus: x = 2 1,41

Ik zou heel graag willen horen of dit ook echt klopt.

Dank, groeten

P.S. Ik zit eigenlijk nog niet op de bovenbouw, maar ik ga er nu naar toe
Bart K
Leerling bovenbouw havo-vwo - vrijdag 19 juli 2002

Antwoord

Beste Bart,

Je aanpak is wel wat erg "grof '
Je hebt het over de omtrek van een cirkel, maar je gebruikt een ingeschreven vierkant, m.a.w. je snijdt af.
Op zich is de methode aardig, maar dan zou je beter 8, 16, 32(enz.) hoeken kunnen gebruiken. Op deze manier is in het verleden de omtrek van een cirkel ook benaderd.
Tegenwoordig weten we dat de omtrek gelijk is aan maal de diameter - 3,14159 Ik neem eigenlijk aan dat je dit ook op school gehad hebt. De diameter is dus het " -de" deel van de omtrek.
Dus diameter=8/ 2,54648
De straal is hier weer de helft van dus 1,27324

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 19 juli 2002