WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Coördinaten van elk punt op een ellips

Met welke formule kan je de cartesische coördinaten bepalen van elk punt op een ellips?
En twee, als je de ellips draait rond zijn middelpunt met een bepaalde hoek, hoe kan je dan terug de coördinaten berekenen?
Het is om een programma te schrijven die de coördinaten weergeeft.
Toelichting:
Je weet de primaire en de secundaire straal (de korte en de lange afstand)om je ellips te tekenen. We draaien de ellips onder een bepaalde hoek (die je zelf kiest) met als rotatiepunt het middelpunt. De enige gekende afstanden zijn die van de korte en de langeafstand. De plaats van het middelpunt mag je vrij kiezen.
Desmet
Iets anders - woensdag 17 juli 2002

Antwoord

Eerst maar eens een plaatje van een ellips om de gebruikte notatie wat duidelijker te maken:

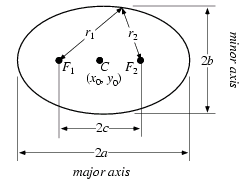
Ik zou de volgende stappen willen voorstellen om tot de formule voor de cartesische coördinaten te komen.

Een ellips is gedefinieerd, zo dat voor elk punt op de ellips de som van de afstanden tot twee vaste punten (de brandpunten) constant is (namelijk de afstand van de straal waar deze twee punten op liggen). Dus r₁ + r₂ = 2a

Om de cartesische coördinaten te berekenen moet eerst de afstand van het middelpunt tot een van de brandpunten worden berekend (afstand c).

Dit kun je berekenen door de rechthoekige driehoek te tekenen tussen de volgende drie punten: het brandpunt, het middelpunt en het snijpunt van de ellips met de straal waar de brandpunten niet op liggen. De lengte van twee van de zijden van deze driehoek is bekend; de derde (c) is dan te berekenen met de stelling van pythagoras.

Nu de afstand van de brandpunten tot het middelpunt bekend is kunnen met de coördinaten van het middelpunt en de hoek van de straal waar de brandpunten op liggen, de coördinaten van de brandpunten worden berekend.

Als de positie van de brandpunten is berekend kan een vergelijking worden opgesteld waarbij de som van de afstand van een bepaald punt op de ellips tot de twee brandpunten gelijk wordt gesteld aan de al eerder bepaalde constante.

Je kunt meer over ellipsen vinden op: http://mathworld.wolfram.com/Ellipse.html
Zie eerder beantwoorde vraag

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 22 juli 2002