WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Constructie cirkel door 2 punten aan een rechte

dag,
Hoe construeer je met passer en liniaal een cirkel die raakt aan een gegeven rechte en door 2 gegeven punten gaat?

groeten,
stef
Stef B
3de graad ASO - zondag 22 mei 2005

Antwoord

We kijken eens hoe het eruit ziet als de cirkel geconstrueerd is.

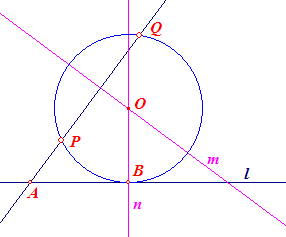
In deze figuur zijn P en Q de gegeven punten en is l de gegeven lijn.
De lijn PQ snijdt de lijn l in het punt A en het raakpunt van de cirkel met l is het punt B.
Als je de plaats van het punt B op l kent, dan kan je met de middelloodlijn m van PQ en de loodlijn n in B op l het middelpunt O van de cirkel vinden.
Naar hoe construeer je het punt B?

In bovenstaande tekening geldt evenwel:
AP · AQ = AB² (... dat moet je natuurlijk wel weten cq. bewijzen!)

En in de hieronder staande figuur geldt: AC² = AP · AQ
(Ook dat moet je natuurlijk weten cq. bewijzen!)

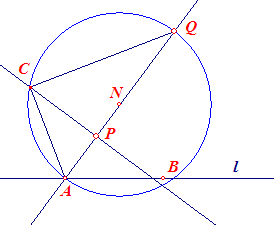
In die figuur is N het midden van AQ (maw. N is middelpunt van de cirkel met AQ als middellijn) en staat de lijn PC loodrecht op PQ (waarom is dan driehoek ACQ rechthoekig?).

Wat weet je dan van AC en AB?

Kan je de constructie op basis van het bovenstaande nu zelf uitvoeren? Natuurlijk!

N.B. Op de lijn l ligt nog een tweede punt B. Er zijn dus twee oplossingen!
Ga zelf na wanneer er slechts 1 oplossing mogelijk is. En wanneer zijn er 0 oplossingen?

Het door jou genoemde constructieprobleem is een deelprobleem van het zogenoemde Raakprobleem van Apollonius (zie onderstaande link).

Zie Raakprobleem van Apollonius

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 22 mei 2005