WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Limiet van een rationale functie

Ik heb al zo veel keren geprobeerd de oplossing van het volgende en het lukt me niet. Kunnen jullie mij misschien helpen? Bedankt

fil
3de graad ASO - vrijdag 6 mei 2005

Antwoord

Het probleem bij deze limiet is dat teller en noemer allebei naar nul gaan, en met 0/0 ben je niet veel.
Maar voor zulke gevallen dient de regel van De L'Hospital.
Die zegt dat de limiet gelijk is aan de limiet dan de afgeleide van de teller gedeeld door de afgeleide van de noemer.

Dus je leidt de teller af naar h, je leidt de noemer af naar h (dat is de afgeleide van h zelf dus dat geeft 1)

En je neemt de limiet van (die nieuwe teller/ de nieuwe noemer).

Het antwoord zou moeten 2/Ö5 zijn.

Koen

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 6 mei 2005

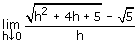
Re: Limiet van een rationale functie