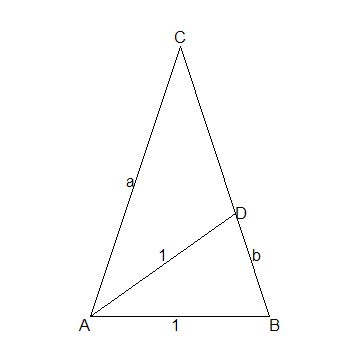|
|
|
\require{AMSmath}



Gulden driehoek
We hebben een driehoek waarvan de onderste zijde AB=1. En de schuine zijdes AC en BC zijn 1/2+1/2 5. 5.
Hiermee moesten we hoek C, dus de hoek van de top berekenen zonder onze grafische rekenmachine te gebruiken. Het antwoord moet 36 graden zijn. De andere twee hoeken zijn dus 72 graden maar dit weten we (nog) niet!
Eva
Leerling bovenbouw havo-vwo - donderdag 28 april 2005
Antwoord
Ik noem het getal 1/2+1/2√5 even a.
Teken op BC een punt D zo, dat AD is 1. BD noem ik b.
Zie onderstaande tekening.
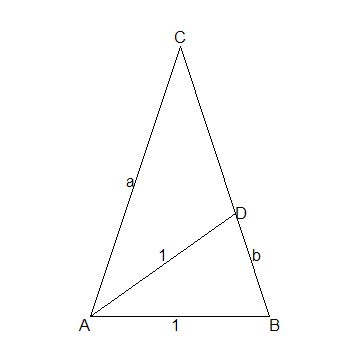
Het is nu vrij eenvoudig in te zien dat driehoek ABC gelijkvormig is met driehoek BDA.
Hieruit volgt vrij eenvoudig dat b=1/a.
Dus b=1/(1/2+1/2√5)=1/(1/2+1/2√5)ˇ(-1/2+1/2√5)/(-1/2+1/2√5)=
(-1/2+1/2√5)/(-1/4+5/4)=
(-1/2+1/2√5)/1=
-1/2+1/2√5.
Dus b=-1/2+1/2√5 en dat is ook gelijk aan a-1!
Dus CD=1.
Nu is driehoek ADC gelijkbenig! Dus hoek C is gelijk aan hoek CAD.
Maar ook (vanwegen de gelijkvormigheid van driehoek ABC en driehoek BDA) is hoek DAB gelijk aan hoek C.
Dus hoek CAD=hoek DAB
Dus AD is de bissectrice van hoek A.
In driehoek ABC geldt dan:
Hoek A=hoek B=2ˇhoek C.
Daaruit volgt: 5ˇhoek C=180 graden. Dus hoek C=180/5=36 graden. (En er volgt ook meteen dat hoek A en hoek B 72 graden zijn)

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 29 april 2005
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 5.
5.