|
|
|
\require{AMSmath}



Variantie en standaardafwijking
In het boek staat een voorbeeld: een fabrikant van elektronica controleert de werking van een onderdeel steekproefsgewijs. Op basis van grote aantallen is de volgende kansverdeling tot stand gekomen.
(Dit staat in het boek dus van boven naar beneden, maar hier van links naar rechts)
aantal defect: 0 1 2 3 4 5 6 >7
de kansen die hierbij horen zijn: 0,41 0,26 0,12 0,11 0,07 0,02 0,01 en 0
Daarna staat er in het boek X-E(X) en bij 0 levert dat volgens het boek 1,6129 op. Ik snap niet wat ze met die X-E(X) bedoelen, wat je er dus mee uitrekent en dus hoe ze aan dat antwoord komen.
De laatste kolom bestaat uit de kans · (X-E(X))2, dat levert bij 0 --> 0,661 op, dat snap ik nog wel, maar op het eind van deze opgave staat ook nog dat E(X) 1,27 is en ook hier geldt dat ik niet snap hoe ze daar nu aankomen.
Sabine
Leerling bovenbouw havo-vwo - maandag 17 juni 2002
Antwoord
In omgekeerde volgorde. E(x) is de verwachtingswaarde, dus als je het aantal defect x noemt en de kans op x noem ik p(x). De verwachtingswaarde is dan:
E(x)=åx·p(x)=0·0,41+1·0,26+2·0,12+...+7·0=1,27
De rest is erg verwarrend. Volgens mij bedoelen ze zoiets als:
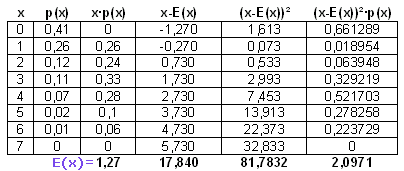
Die 2,09 is de variantie... als je daar de wortel van neemt krijg je de standaarddeviatie.Hopelijk help dat...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 17 juni 2002
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










