WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Lengte van een kromme + inhouden

(1)
Bereken de booglengte van y= (e^x+e^(-x))/2 wanneer xÎ[0,1]

Ik probeerde:
f'(x)=(1/2)(e^x-e^(-x))

L=òÖ((1/4)(e^(2x)+(1/e^(2x))+1-(2e)/4)dx

Hoe kan ik deze integraal op een correcte manier oplossen?

(2)
Bereken de booglengte van y=x², als xÎ[0,1]

Ik probeerde:
f'(x)=2x

L=òÖ(1+4x²)

ik gebruikte goniometrische substitutie:
2x=tant
2dx=dt/cos²t

= ò(1/cost)(dt/2cos²t)= (1/2)ò1/cos^3(t) dt = ?? Mocht er cos^3(t) in de noemer staan zou dat nog opspiltsbaar kunnen zijn maar...

(3)
Men laat een vlakke figuur, begrensd door y=xe^x, de x-as en de rechte x=1, wentelen om de x-as. Bepaal de inhoud het ontstane lichaam.

Ik probeerde:
I=pò(x.e^x)dx
-- ò(x.e^x)dx = (x-1)e^x + c (via partiële integratie)

Maar hoe kan ik dan I bepalen want ik blij zitten met een ò(x.e^x)dx zelfs na de partiële integratie?

Kan iemand me opnieuw verder helpen aub?

Dank bij voorbaat en vele vriendelijke groetjes.

Veerle
3de graad ASO - vrijdag 8 april 2005

Antwoord

Beste Veerle,

1) Je afgeleide is goed, maar de integraal die je dan opschrijft volg ik niet helemaal...
Ik vermoed dat je voor een booglengte deze formule gezien hebt:
ò(a-b Ö(1 + f'(x)²) dx

Hier even een uitwerking, uitleg eronder:

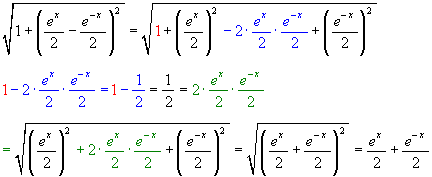
Ik werk eerst het kwadraat uit volgens (a-b)² = a² -2ab +b²
In de tweede regel reken ik verder met het blauwe en rode gedeelte. Je ziet dat het blauwe gewoon -1/2 wordt, maar met die 1 dus +1/2. Dit is dus het tegengestelde van wat er eerst blauw was, en dus terug een dubbel product: maar dit keer met een plusteken. We kunnen dus nu terug via a² +2ab +b² naar (a+b)².
Het kwadraat valt tegen de wortel weg en we vinden de oorspronkelijke functie! (en niet de afgeleide)

Integreren lukt dan wel?

2) In een van je vorige vragen moest je een gelijkaardige integraal uitrekenen, namelijk ò1/sin³x dx
Toen lukte het met de t-formule (x = tan(t/2)), dat zal hier ook gaan maar iets ingewikkelder worden...

3) Vergeet je niet te kwadrateren?
De formule voor een omwentelingslichaam is toch pòf(x)² dx...

Je zal er waarschijnlijk wel partiële integratie nodig hebben.

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 8 april 2005

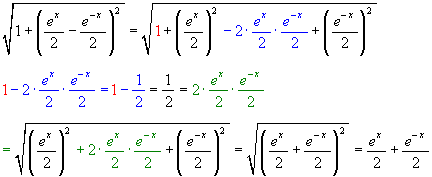
Re: Lengte van een kromme inhouden