WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Constructie van een vijfhoek

Hoi,

Ik moet het volgende bewijzen (met complexe getallen) en ik geraak niet op weg:

Een tekening:

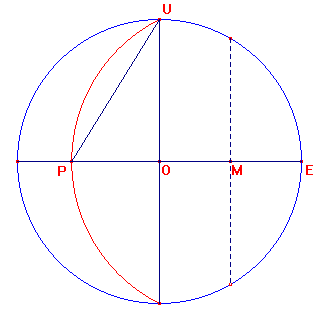
M is het midden van OE
PM=UM
Te bewijzen:
UP is de lengte van de zijde van een regelmatige vijfhoek en PO is de lengte van de zijde van een regelmatige tienhoek.

Veel dank
Jeroen
Student Hoger Onderwijs België - vrijdag 14 juni 2002

Antwoord

Wat de link met complexe getallen is zie ik niet zo 1-2-3, maar een 'gewoon' meetkundig bewijs mag misschien ook nog wel?

Ik neem aan dat je al ergens gezien hebt dat de zijde van een regelmatige vijfhoek in een cirkel met straal r gelijk is aan
½ . r . (10 - 2.5)
(zo niet, dan meld je je nog maar een keer)

Het komt er nu dus op aan om aan te tonen dat PU deze lengte heeft. Voor het gemak nemen we r = 1.

PO = PM - OM = UM - OM = 1¼ - ½ = ½.5 - ½

PU² = PO² + OU² = 1½ - ½5 + 1 = 2½ - ½5

Conclusie:

PU = (2½ - ½5) = ½(10 - 25) hetgeen bewezen diende te worden.
Als je niet precies ziet waarom deze wortelvormen aan elkaar gelijk zijn, dan kun je ze óf eens intikken in je rekenmachine (al zegt dat eigenlijk niks!) óf de vormen eens kwadrateren. In het laatste geval zal er tweemaal hetzelfde gevonden moeten worden.
En in noodgevallen kun je het natuurlijk ook nog eens aan Wisfaq vragen!
Overigens is OP de zijde van de regelmatige 10-hoek en de lengte heb je hierboven ook berekend.

MBL

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 15 juni 2002

Re: Constructie van een vijfhoek